שיטות חדשות לאפיון התקנים לא ליניאריים

Malcolm Edwards,
AWR Corporation

פיתוח מודלים אנליטיים ואמפיריים הציב מאז ומעולם אתגר מתסכל בפני מתכנני מעגלים לתדירות גבוהה. פיתוח מודל הוא תהליך יקר וגוזל זמן, שעלול לחשוף נכסים אינטלקטואליים של היצרן, והתוצאה המתקבלת יכולה להיות שונה באופן משמעותי מיצרן אחד למשנהו. בנוסף, בשל הדרך שבה מופקים רוב הפרמטרים של המודלים הקומפקטיים, קיים ספק לגבי יכולתם לחזות את ההתנהגות בתנאים לא ליניאריים קיצוניים או עם סיומות שאינן 50 אוהם.
הפיתוחים שנעשו לאחרונה בטכנולוגיה של מדידות ויצירת מודלים מתמקדים במודלים של “קופסה שחורה” שאינה תלוית טכנולוגיה אך מבוססת מדידות. תפיסה זו מאומצת על ידי מפתחי תוכנה ויצרני ציוד בדיקה. מאמר זה בוחן את המודלים ומערכות המדידה הלא ליניאריים השונים שקיימים כיום ואת הדרך שבה אפשר להשתמש במודלים אלו עם תוכנת התכנון לתדירות גבוהה Microwave Office של AWR.
מודלים של התקנים ליניאריים ולא ליניאריים הם אבני היסוד של רוב התכנונים בת”ר (RF) ובגלי מיקרו, ופרמטרי S מייצגים התקנים ליניאריים. כמודלים של “קופסה שחורה”, אפשר להשיג אותם בקלות באמצעות נתח רשתות ווקטורי לצורך הדמיה. הם משתמשים בסופרפוזיציה להשוואת היחס הליניארי בין הגל הפוגע והגל המוחזר בכל חיבורי ההתקן. מצד שני, התקנים לא ליניאריים מעוותים צורות גלים כך שלא ניתן לייצג את התנהגותם באמצעות סופרפוזיציה או פרמטרי S.
מודלים לא ליניאריים מתארים טרנזיסטורים, לרבות אזור האותות הגדולים שבו פועלים מגברי הספק. מודלים להתקני אותות גדולים מתפתחים בקביעות כדי להתעדכן בשינויי טכנולוגיית המוליכים למחצה. קבוצה תעשייתית מתחום המוליכים למחצה וכלי התכנון הקרויה מועצת המודלים הקומפקטיים (CMC) פועלת למען יצירת סטנדרטיזציה של פרמטרי המודלים. יעד קשה להשגה ורב ערך הוא חיזוי של ביצועי המעגלים בדור הבא וזיהוי הכיוון לפיתוח מודלים לתמיכה בהם.
לצורך כך יש צורך לבחור בתנאי פעולה שמגדירים אופייני התקן לא ליניארי, לשכפל את ההתנהגות הזו ולהפיק את הפרמטרים עבור משוואות מודל אלו. לחלופין, במקום מודלים סטנדרטיים או מתפתחים אפשר להשתמש בנתונים הנמדדים ישירות בדומה להתקנים ליניאריים או של פרמטרי S. זו הגישה העומדת בייסוד הרחבת פרמטרי S הליניאריים לצורה כללית יותר של תיאור התנהגות לא ליניארית. במקום בטבלת פרמטרים, עבור המשוואות משתמשים בנתונים המבוססים ישירות על התנהגות ההתקן הנמדדת עם עירור מסוים וקבוצה של עכבות (“אימפדנסים”) חיבורים.
מודל “הקופסה השחורה” מבוסס המדידות עומד מאחורי המודלים המסחריים העכשוויים, הידועים כמודלים התנהגותיים לא ליניאריים, למשל X–parameter, S–functions, מודל Cardiff ואחרים. שני הראשונים הם הרחבות של גישת המודל PHD שפותח על ידי Verspecht ועמיתיו. הם מייחסים את הספקטרום שבחיבורי ההתקן לקבוצה נתונה של אותות עירור ועכבות סיומת. מודל Cardiff שפותח על ידי Tasker ועמיתיו, הוא מודל דומה מבוסס טבלה, שמתייחס לנתוני צורות גלים IV בחיבורי ההתקן עבור אותות עירור נתונים וקבוצות של עכבות עומס ומקור.
מודלים מתפתחים אלו וטכניקות המדידה הנדרשות להפקתם מסכמים כ-20 שנות מחקר ופיתוח מסחריים ואקדמיים. ספקי ציוד בדיקה מציעים מערכות המיועדות לאפיון לא ליניארי בגלי מיקרו. מערכת של חברת Tektronix מבוססת על גישת משקף תנודות (אוסצילוסקופ) דגימה, לעומת מערכות אחרות המבוססות על טכניקות של נתחי רשתות לא ליניאריות ווקטוריים. החברות Anritzu, Rohde & Schwarz ו–Tektronix מיצבו עצמן עם טכנולוגיות HFE Sagi, NMDG ו–Mesuro כדי לפתח את טכנולוגיות יצירת המודלים במדידה הלא ליניאריות שלהם.

התנהגות לא ליניארית
ניתן לייצג אות מחזורי (CW או מאופנן) במישור הזמן או במישור התדר. כאשר אות כזה דוחף התקן לאזור הלא ליניארי, צורת הגל IV מתעוותת ולא ניתן לתאר אותה רק באמצעות הפעלת גורם מכפיל על אות הכניסה. במישור התדר ניתן לייצג את ההתנהגות הזו על ידי השינויים בהרמוניות של הרכיבים הספקטרליים ובאפנון ההדדי שלהם כפונקציה של אותות העירור ושל עכבות החיבורים. חשוב ביותר שהמודל הלא ליניארי ישכפל את ההתנהגות הזו עבור כל אות מעורר וכל עכבת חיבור.
גישת העיוות בריבוי הרמוניות ליצירת מודלים מבוססת על מדידות במישור הזמן. התדר הבסיסי הוא העיקרי והתדרים של ההרמוניות קטנים באופן יחסי, כך אפשר להפעיל במדויק את עיקרון הסופרפוזיציה של ההרמוניות. לפי העיקרון, גודל אותות בדיקה קטנים מאפשר להתייחס להפרעה כאל תהליך ליניארי.
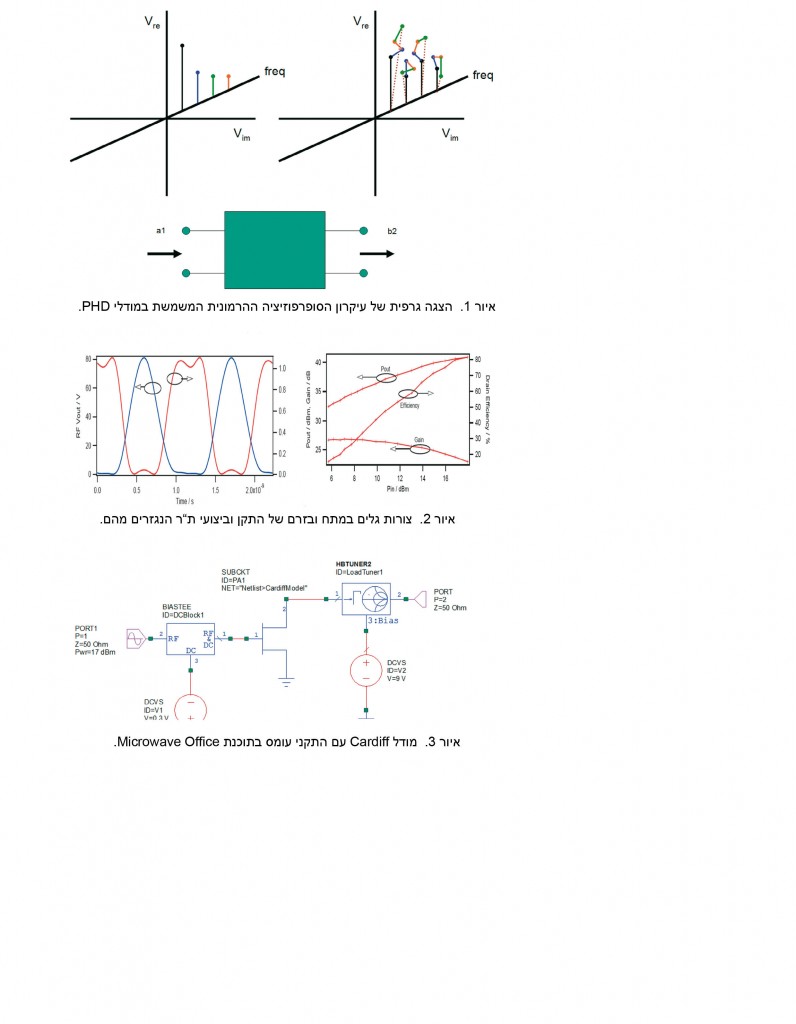
עיקרון הסופרפוזיציה של הרמוניות מוצג באיור 1 בצורה גרפית. התדר הבסיסי שדוחף את היחידה הנבדקת למצב פעולה לא ליניארי מיוצג על ידי התדר השחור שבאיור. אפשר לראות את הרכיבים ההרמוניים שנוצרו (בשחור) בחיבור היציאה. אות הבדיקה הקטן הראשון –תדר ההרמוניה השנייה (בכחול)– מוזרק לתוך Port 1 ויוצר הפרעה של ארבעת התדרים. אות הבדיקה הקטן הבא –ההרמוניה השלישית (בירוק)– מוזרק שנית לתוך Port 1 ושוב גורם להפרעה בארבעת התדרים. תהליך זה נמשך עד אשר כל ההרמוניות וכל חיבורי port הובאו בחשבון.
עם חיבור היחידה הנבדקת לנתח רשת לאותות גדולים (LSNA) נוצר באופן אוטומטי מודל המתאר במדויק את כל היבטי ההתנהגות הלא ליניאריים, כגון המשרעת (אמפליטודה) והפאזה של ההרמוניות, אופייני דחיסה, AM–PM, שחזור ספקטרלי, כניסה תלוית משרעת ותיאום יציאה. גישה זו מספקת יותר ממספרים, למשל Psat ונקודת פגישה (intercept) מסדר שלישי. אפשר להשתמש במודל PHD בסביבת EDA לתיאור עקבי של אופיינים לא ליניאריים ובתכנון ואופטימיזציה של מעגלים עם התקנים לא ליניאריים.
S–functions ו–X–parameters הם מימושים מסחריים של מודל PHD ומאחר שהם ממקור אחד, ובדרך כלל מיועדים לאותן מערכות, הם מקובצים יחד. ההבדלים המשמעותיים בין הגישות ייעלמו בעתיד, לאחר שהטכנולוגיות ימוזגו.

S–functions
S–functions הן הרחבה של S–parameters עבור רכיבים לא ליניאריים, והם מאפשרים להאיץ את התכנון של מערכות עם רכיבים לא ליניאריים. הן מאפשרות לחזות התנהגות של התקנים לא ליניאריים בתנאים שונים של חוסר תיאום. בדומה ל S-Parameters, ניתן לחבר את S–functions בטור. כדי לחזות התנהגות לא ליניארית של מעגלים ומערכות. הן נקבעות בקלות עם אפשרות יצירת המודלים של ערכות NMDG VNAPlus, שהן הרחבה של נתחי Rohde & Scwartz, באמצעות חומרה ותוכנה נוספים לאפיון התנהגות לא ליניארית.
האפיון מתבצע במישור התדר ואפשר להמיר אותו למישור הזמן לתנאים מציאותיים עבור כל עכבת חיבור באמצעות מדידות עומס/ מקור. Microwave Office יכולה לייבא את מודל ההתנהגות הזה כדי לתכנן ישירות מעגלים גדולים יותר בעזרת הנתונים שנמדדו או לספק דפי נתונים מפורטים יותר.

מודל Cardiff
מערכת המדידות של Cardiff והמודל הקשור אליהם משיגים בחיבורים של היחידה הנבדקת את צורות הגלים הפוגעים והמוחזרים של הזרם והמתח במישור הזמן. מערך הבדיקה דומה לנתח רשתות ווקטורי, אך הוא משתמש במשקף תנודות דוגם במקום בערבול או בדגימה במישור הזמן. המודל שנוצר משתמש בארבע פונקציות מבוססות טבלה שמייצגות את התנהגות ההתקן בעירור כניסה, הגבר ועכבת סיומת שנתונים, באמצעות הזרמים והמתחים המתוקנים שלו. המערכת יכולה להשתמש במדידות של אות גדול בתדר יחיד או בריבוי תדרים.
על ידי שליטה בסיומות העומס בכל תדרי ההרמוניות, במקביל לאפשרות הצפייה בצורות גלי המתח והזרם במישור יצירת הזרם של ההתקן, המתכנן יכול לעצב את צורת הגל באופן כזה שתתאים לערכים התיאורטיים להפקת תוצאות אופטימליות. אפשר להפיק בתוך Microwave Office את המודל ההתנהגותי שנוצר בתנאי העומס של הביצועים האופטימליים, ומכאן שאפשר לאפיין באופן מלא התקנים או מגברי הספק עבור כל רמת אות וכל סביבת עכבות. עבור קבוצת תנאי סביבה מסוימת, מודל כזה אמור להיות הצגה מדויקת יותר מאשר מודלים שנוצרו מחוץ לפרמטרי הפעולה האלו.
Wright, Heikh, Roff, Tasker ו–Benedikt הראו במאמרם כיצד שימשה הנדסת צורות גלים כדי לבצע אופטימיזציה של מגבר הספק Class–F מהופך, למען השגת נצילות drain גבוהה יותר מ–81 אחוזים, הספק מוצא של 12 וואט ב–900 וב–2100 ג’יגה–הרץ באמצעות טרנזיסטור HEMT בטכנולוגיית GaN כפי שמוצג באיור 2. יכולת זו מאפשרת למתכננים להבין מהם הביצועים שאליהם יכול להגיע ההתקן שבידם עם רשתות התיאום הנכונות.
על מנת לתכנן את הרשתות האלו או כדי לחבר התקנים למגברים בריבוי דרגות נדרשת סביבת הדמיה, שאותה אפשר ליצור על ידי הצגת האופן שבו פועלת תוכנת Microwave Office עם סוגי מודלים חדשים אלו. מודל Cardiff משולב בתוך ההדמיה של Microwave Officeבאמצעות רכיב מבוסס רשימת רשת (איור 3) המקושר לטבלת נתוני המתח והזרם במודל Cardiff דרך תבנית העברת נתוני גלי המיקרו או בקובץ MDIF (איור 4)

ניתוח אפנון הדדי
בריבוי תדרים
על מנת להבטיח שניתן יהיה לפתור בעיה מסוימת, יש לקצץ את קבוצת תדרי האפנון ההדדי, כדי להגביל את מספר התדרים הנדרשים לפתרון אלגוריתם HB. המשתמש מבצע את כל זאת בחלון ההגדרות של המדמה של Microwave Office. במימושים קיימים של המודלים ההתנהגותיים הלא ליניאריים אין תמיכה מפורשת בתיאור FDD לריבוי תדרים במובן של אפנון הדדי. המשמעות היא שאין דרך קיימת לביצוע חקירה ישירה של ריבוי תדרים סביב התדר הראשי.
עם זאת, אפשר להשתמש בשיטות אחרות, שאינן ישירות, (פותרי מעטפת מורכבת או מעטפת מעגל), על מנת לחקור אפנון הדדי, וכל אחת מהן מתייחסת להנחות מסוימות. שתי השיטות משתמשות במודל במידע AM–AM ו–AM–PM ויוצאות מהנחה שההרחבה הספקטרלית היא כזו שהשפעות האפנון ההדדי נמצאות בפס צר ומרכזן בגל הנושא. עובדה זו לא נחשבת מגבלה שמונעת את האפשרות להשתמש בהן למשימה זו. לכל המודלים יש מגבלות והם נמצאים בדור הראשון שלהם עם פיתוח שנמשך בתחומים של מדידות, הפקת נתונים, תמיכה בהדמיות והיקף היישום.

סיכום
תוכנת Microwave Office של AWR יכולה לבצע הדמיה של מודלים לא ליניאריים מבוססי מדידות וכן של המודלים מבוססי הטבלאות המשמשים כיום, כמו S–function, X–parameters ו–Cardiff. מתוך התוכנה יש ייחוס אל נתוני המודל המאוחסנים בקובץ MDIF באמצעות רכיב מבוסס רשימת רשת. ההתייחסות במדמה אל מודלים ספקטרליים כגון S–function ו–X–parameters היא כאל התקנים במישור התדר ומתבצעת באמצעות מיפוי ספקטרלי. סוגי מודלים אלו מבטלים את הצורך לפתור את ההתקנים הלא ליניאריים במישור הזמן וכן את הצורך לאזן מבחינת ההרמוניות את הענפים הליניאריים והלא ליניאריים של רשת ההדמיה.

*הכתבה נמסרה באדיבות RDT, נציגתה הבלעדית של חברת AWR בישראל.