אחת הסיבות העיקריות לשימוש הלקוי במדמי תופעות אלקטרו–מגנטיות (EM) ובתוצאות שהם מפיקים, היא אי הבנה של הדרך שבה מממשים את ההארקה בהדמיות מעגלים. מאמר זה מגדיר את המימוש הזה ומסביר כיצד יש לבחור את אפשרויות ההארקה המוצעות במדמים. מדמים מודרניים רבים תומכים בהארקה מקומית, שבה אפשר להשתמש בהגדרות הארקה שונות לנקודות שונות. תכונות חדשות במדמה אלקטרו–מגנטיות המישורי התלת–ממדי AXIEM 2009 של AWR מציעות אפשרויות מקיפות למקורות ולחיבורי port, וכן לביטול ההשפעות של התקן המדידה (de–embedding). נבין כיצד משמשת הארקה בהדמית מעגלים, נבחן את האופן שבו מוגדרת ההארקה במדמי אלקטרו–מגנטיות, נסביר מדוע זו פונקציה של הפותר (solver) ושל סוגי החיבור ונסקור כמה דוגמאות ברמת המעגל, המארז והשבב.
הארקה יוצרת בסיס חשוב לדרך יצירת מודל וביצוע הדמיה של קווי תמסורת. הדרך שבה מנתחים במעגלים אמיתיים “מהי הארקה” ו”היכן היא”, משתנה בהתאם לבדיקת הפיסיקה העומדת בבסיסה. AXIEM תוכנן מתוך מחשבה לספק גמישות כזו, והוא מאפשר למתכנן להגדיר את מיקומה של הארקת הייחוס בתכנון, כך שבעת הוספת חיבור port המתכנן יוכל לייחס את החיבור לאותה הארקה, בלחיצת עכבר. במקרה של מוליך גלים במישור משותף (coplanar), המתכננים יכולים גם להגדיר מערכת חיבורים שתייצג נאמנה את התקדמות הגל ואת “חזרת” הזרם, באמצעות קבוצות חיבורים. הכלי מאפשר לקבוע כיצד יבוטלו השפעות המדידה בחיבורים ומעניק למתכננים ביטחון שהם מודדים את המבנה כשההארקה נמצאת במקום שאליו התכוונו, ללא תופעות שווא של החיבורים וללא צורך בהגדרות גיאומטריה שנדרשות לפותר.
הארקה בהדמית מעגלים
סטודנטים לחשמל ולאלקטרוניקה לומדים שעליהם להתייחס למתח ולזרם, והם מקבלים את שני חוקי קירכהוף כעובדה: סיכום הזרמים (עם סימן) בכל צומת שווה לאפס, וסכום המתחים בכל לולאה שווה לאפס. מאחר שסכום המתחים בלולאה, כלומר הפרש המתחים, הוא הקובע, קיימת נקודה אחת במעגל במתח אפס, שהיא ההארקה ומכונה במדמים “צומת 0”. הסטודנטים לומדים מעט מאוד באשר למהות ההארקה ומדוע היא חשובה.
ההגדרה האלקטרו–מגנטית של ההארקה
חוקי קירכהוף נגזרים ממשוואות מקסוול, ואכן שימור המטען נגזר מחוקי אמפר וגאוס לשדות חשמליים:
כאשר הסכום הוא הזרם נטו שנכנס לצומת והצטברות המטען בה הוא Q. בתיאוריית מעגלים רגילה, מטען יכול להצטבר רק בקבלים, ומכאן שסכום הזרמים בכל צומת חייב להיות אפס, ובקבלים Q=CV.
מושג המתח המשמש במשוואת הקבל הוא גודל נגזר, שכן אינו חלק ממשוואות מקסוול שבהן קיימים רק שדות מגנטיים, צפיפות זרם וצפיפות מטען. אפשר לגזור גדלים פיסיקליים אחרים מהמשוואות תוך שמירה על עקביות חוקי הפיסיקה.
מתח מוגדר כאינטגרל של שדה חשמלי לאורך מסלול (למעשה רק של החלק המשיק למסלול). חשיבות הגדרה זו נעוצה בחוק פאראדיי, שלפיו השדה החשמלי במסלול סגור (לולאה) שווה לשינוי בזמן של השטף המגנטי דרך לולאה זו (בסימן מינוס):
כאשר E הוא השדה החשמלי, F הוא סך כל השטף של צפיפות השדה המגנטי, B, בלולאה. מכאן שהשינוי במתח בלולאה שווה לשינוי השטף המגנטי בלולאה (בסימן מינוס). ההנחה בתיאוריית המעגלים היא, ששינוי השטף המגנטי דרך לולאה קטן דיו כדי שייחשב אפס, ולכן השדה החשמלי, וגם המתח, הם אפס סביב כל לולאה, וזה חוק קירכהוף.
קיים תחום בו אין אפשרות להתעלם מהשטף המגנטי לגבי השראות והגדרתה:
כאשר השטף F נוצר על ידי הזרם I.
שים לב שחוקי קירכהוף נובעים מבחינה לוגית ממשוואות מקסוול, בדומה למונחים קיבול והשראות. ההנחה שערכיהם קטנים דיים מאפשרת לדון במעגל אידיאלי.
לסיכום, מאחר שהמתח סביב לולאה הוא אפס, אין הוא תלוי במסלול, ולכן אפשר לבחור נקודה במעגל שתיחשב 0 וולט ולכל נקודה במעגל לתת ערך של מתח, והוא יהיה ביחס להארקה.
הדמיית מעגלים, פרמטרי S והמונח הארקה
מדמי מעגלים מתבססים על פתרון משוואות קירכהוף. הם פותרים משוואת מטריצות וקובעים את המתחים והזרמים בכל הצמתים שבמעגל. המדמים המודרניים קובעים את המשוואה באמצעות ניתוח צמתים משופר (Nodal Modified Analysis) שבאמצעותו נוצרות משוואות קירכהוף עבור כל צומת, והמטריצה נפתרת בטכניקות רגילות. המדמים משתמשים במטריצות Y לתיאור פעולת רשתות המשנה, וכל רשת נחשבת לאוסף צמתים חיצוניים המיוחסים ביניהם.
מהנדסי ת”ר (RF) וגלי מיקרו מעדיפים לרוב להשתמש במטריצות פרמטרי S, המשמשות במדמי אלקטרו–מגנטיות, ואותן יש להמיר למטריצות Y, המשמשות במדמי מעגלים, כלומר המדמים חייבים להשתמש במתחים ובזרמים. לצורך כך נדרשות העכבות (אימפדנסים) האופייניות של חיבור port. פרמטרי S במובנם האמיתי הם יחסים בין הספקים, ואם העכבות הן ערכים מרוכבים ידועים, אפשר להמיר את ההספק לזרם ומתח ולהפיק את מטריצת Y. המשוואה לכך היא:
כאשר S הוא מטריצת S, I הוא מטריצת הזהות ו–Zg הוא המטריצה האלכסונית שהאברים שבה הם העכבות האופייניות לכל חיבור, אשר יכולות להיות מספרים מרוכבים.
חיבורי port במדמי אלקטרו–מגנטיות
לכל מדמי האלקטרו–מגנטיות נדרשים חיבורי port כדי לגזור פרמטרי S. לתוך המערכת מזריקים אנרגיה (גלים) דרך החיבורים, ומודדים את ההספק המוחזר לחיבורים והמועבר לחיבורים אחרים. היחס בין ההספק המוחזר או ההספק המועבר לבין ההספק המוזרק, הוא בהגדרתו, פרמטר S. מניחים שכל החיבורים נמצאים בתיאום מושלם – אות שמוזרק לחיבור לא יוחזר פעם נוספת לתוך המערכת. ההנחה הקיימת בהעברת פרמטרי S ממדמה EM למדמה מעגלים היא שיש הארקה אחת לכל החיבורים, לכן חשוב לדעת באיזו הארקה משתמש כל חיבור.
העולם של מדמי אלקטרו–מגנטיות
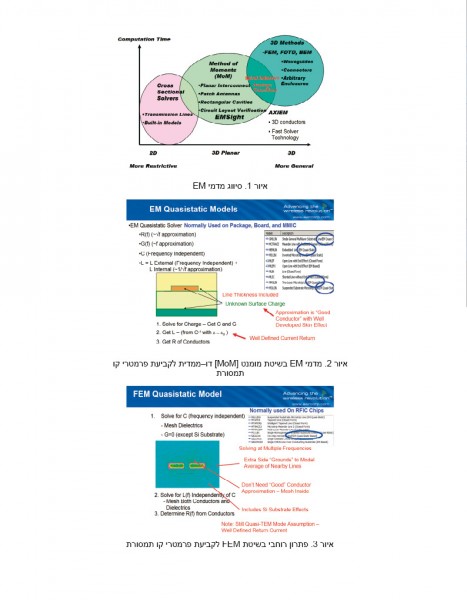
מדמי אלקטרו–מגנטיות (EM) פותרים את משוואות מקסוול באופן נומרי. קיימות דרכים רבות לסווג מדמי EM למשל לפי הטכניקות המתמטיות, לפי הכלליות של הבעיות שהם פותרים, לפי מהירות ההדמיה ולפי תכונות וממשק המשתמש. לדיון זה המדמים יסווגו לפי איור 1.
הציר האופקי משווה באופן גס את כלליות הבעיות שאותן המדמים מכסים. בציר האנכי מתוארת המורכבות החישובית. המדמה הכללי ביותר מתואר כאן כתלת–ממדי (3D) והוא המקיף ביותר מבחינה חישובית.
סוג הפותרים המתואר כדו–ממדיים (2D) או כמיועד לניתוח רוחבי (cross sectional) משמש לקבלת פרמטרי קו תמסורת ליחידת אורך במערכת קווי התמסורת. למשל הפותר ייחשב התנגדות, קיבול, השראות ומוליכות עבור יחידת אורך של קו microstrip, ולאחר שהתכונות החשמליות ליחידת אורך, ונתוני האורך של קו תמסורת יהיו ידועים, קל יהיה להכפיל אותם לקבלת פרמטרי הקו ולהשתמש במודל קו פרוס (distributed line model). מדמים כאלו משולבים לעתים קרובות במדמי מעגלים ופועלים ברקע, כמו למשל בתוכנה Microwave Office® של AWR. מדמים אלו מתחלקים למשתמשים בטכניקת שיטת המומנט (MoM) ולמשתמשים בטכניקת האלמנטים הסופיים (מוצגת באיור 2).
הזרמים והמטענים על גבי המשטח מחושבים בטכניקת MoM ומספקים את הקיבול ואת ההשראות ליחידת אורך. המודל מאפשר לחשב את הערכים בתדירות אחת בלבד, אך מניחים שהקיבול לא משתנה בתדירות וההתנגדות וההשראות משתנים לפי השורש הריבועי של התדירות. ההנחה מבוססת על קירוב עומק הקרום (skin depth), על פיו המוליכים עבים דיים כדי להכיל כמה קרומים. עובי הקרום בנחושת ב–1 ג’יגה–הרץ הוא מיקרון אחד, לכן יש תוקף להנחה זו בקווי נחושת במעגל, שעוביים עשרות מיקרונים. מדמה MoM מציב את משטח ההארקה בתחתית מבנה קווי microstrip.
סוג אחר של פותר רוחבי המשמש בתוכנת Microwave Office פועל בשיטת האלמנטים הסופיים (FEM) המוצגת באיור 3. בשיטה זו, שגם בה מתקבלות תכונות קו התמסורת ליחידת אורך, משלבים את חתך הרוחב ברשת משולשים ופותרים את השדה החשמלי לכל אחת מהרשתות. היתרון בטכניקה זו הוא שאפשר לחשב הפסדים והשראויות פנימיות בקווי התמסורת, בלי צורך בהנחה לגבי עומק הקרום, והוא מתבטא בבדיקת שבבים שבהם אין אפשרות לקבוע את עובי הקרום. ההארקה בהדמיות מסוג זה היא המוליך התחתון בסיליקון והדפנות הצדדיות בקצה מרחב האלמנט הסופי.
הסוג הבא של מדמי EM המוצג באיור 1 הוא מדמים מישוריים תלת–ממדיים, שנקראים גם מדמי שניים וחצי ממדים. מדמים אלו משתמשים בשיטת MoM שבה משלבים את קווי המוליכים לסדרת משולשים ומלבנים. הזרמים מחושבים באמצעות מטריצה, ועירור שלהם מאפשר חישוב של פרמטרי S. בשיטה זו מחושבים זרמים מישוריים וזרמים אנכיים בחורי מעבר ובמוליכים עבים. המגבלות הגיאומטריות של השיטה נובעות מהמבנה המישורי והאחיד של השכבות הדיאלקטריות עם משטח הארקה בתחתית, ואולי משטח מוליך עליון. ברוב המקרים אין זו בעיה בעולם המעגלים, המארזים והשבבים. המבנה יכול להיות בתיבה משולשת מוליכה או ללא תיבה, בתלות בקוד.
מדמי EM מהסוג השלישי מתוארים באיור 1 כתלת–ממדיים והם יכולים לבצע הדמיה של רוב המבנים, מאחר שהם משלבים ברשת את כל המרחב הרצוי באמצעות יחידות קטנות. יחידות אלו הן בדרך כלל פירמידות משולשות (טטראדר) או לבנים מלבניות. השיטות המקובלות לפתרון השדות הן FEM במישור התדר ו–FDTD (ההפרש הסופי במישור הזמן). מאחר שאנו עוסקים בהארקה, לא נדון בהבדלים הטכניים הקטנים שבין השיטות השונות. כמו כן יש לציין שקיימות שיטות נוספות לפתרון בעיות תלת–ממדיות. הפותרים התלת–ממדיים כלליים יותר ומקיפים יותר בחישובים מאשר הפותרים המישוריים התלת–ממדיים, יש בהם פשרות ואין פותר תלת–ממדי אחד שמתאים לכל היישומים.
מדמים תלת ממדיים וחיבורי port
מדמים תלת–ממדיים פותרים את השדות החשמליים שנמצאים בתוך מרחב מוגבל בקצות מרחב ההדמיה. המרחב משובץ ברשת של צורות קטנות ופשוטות, בדרך כלל, טטראדרים או מנסרות מלבניות. לשדה החשמלי יש צורה מקורבת פשוטה בכל אזור. השדות מעוררים דרך חיבורי port ולאחר מכן מחושבים, כפתרון של משוואות מקסוול בתנאי הגבול הנכונים.
נתחיל את הדיון בחיבורי port במדמים תלת–ממדיים באנלוגיה לנתח רשת. הנתח פועל על ידי משלוח גל דרך חיבור לתוך קו תמסורת, כגון כבל קואקסיאלי. הגל המשודר נכנס ליחידה שבבדיקה (DUT) וההספק שלו מוחזר ומתקבל S11, משודר לחיבור השני ומתקבל S21, או מתפזר. פיזור אנרגיה נעשה בבליעה או בהקרנה ביחידה הנבדקת או בבליעה בחיבור השני, שבו יש סיומת עומס מתואם.
חיבור port יכול להיחשב לפאת הקצה של מוליך גלים שקצהו השני הוא נתח הרשת. הנתח מתואם לחלוטין למוליך הגלים. גלים במוליך גלים מתוארים לפי מצבים. למשל, בקו תמסורת, המצב העיקרי הוא אלקטרו–מגנטי ניצב (TEM). מצבים מסדר גבוה יותר נקטעים בתדירויות הפעולה הרגילות. אפשר לאפיין מצבים על פי שלוש תכונות: תבנית השדה, העכבה האופיינית וקבוע ההתפשטות.
התבנית נקבעת על ידי משוואות מקסוול. לחיבור הגל יש גבול חיצוני שמשפיע על הפתרון. לדוגמה קו microstrip באיור 4 פועל במצב דמוי TEM, מאחר שיש רכיבי שדות חשמלי ומגנטי קטנים בכיוון ההתקדמות. הזרם זורם לאורך הקו רחוק מהדפנות ומהחלק העליון ומוחזר מההארקה שמתחתיו והתוצאה היא מצב microstrip. הבדלים חמורים ייווצרו בין המצב בפועל למצב זה אם הדפנות יהיו קרובים מדי. מצד שני, אם הם רחוקים מדי, מתבזבזים משאבי חישוב וטעויות עלולות להתרחש. כלל “אצבע” אומר להרחיק את דפנות הצד והחלק העליון למרחק שהוא פי שלושה מגובה המצע.
חישוב פרמטרי S נעשה לאחר חישוב כל המצבים הנחוצים באמצעות משוואות מקסוול וקביעת המצבים העצמיים (eigenmode) והערכים העצמיים (eigenvalue). הערכים העצמיים הם מספרי הגלים, g , של המצבים:
b הוא קבוע הפאזה השווה ל– 2p/l. הוא קבוע הדעיכה ב–Np/m, וכאשר אינו אפס, הגל דועך במעבר דרך הקו. המצב העדיף, שבו b גדול ככל האפשר ו–a קטן ככל האפשר, הוא המצב הקרוב ביותר ל–TEM ונקרא מצב 1. החישובים שמתבצעים על ידי התוכנה עם הזרקת אותות מאפשרים לחשב את פרמטרי S. בשיטה זו אין צורך בהארקה מפני שמשתמשים בהתפלגות מודאלית ובהספקים, ואלו הן תפישות אלקטרו–מגנטיות. הצורך בהארקה קיים בשימוש בעכבה אופיינית שאין לה הגדרה בהקשר של מוליך גלים.
אפשר לקבוע את ההספק העובר דרך מוליך גלים מהשדות החשמלי והמגנטי, ואפשר למצוא את הזרם בכל מוליך בהיותו יחסי לשדה המגנטי המשיקי למוליך (עיין באיור 5).
אחת ההגדרות של עכבה משתמשת ביחס שבין סך כל הזרם להספק במוליך:
שים לב שההספק נטו במוליך הגלים הוא אפס, כלומר, יש הספק הזורם בכיוון ההפוך. הסיבה לכך נראית באיור 6: השדות החשמלי והמגנטי במוליכים החיצוניים הם אפס ואינטגרל השדה המגנטי סביב לולאה ההולכה החיצונית הוא אפס. לפי חוק אמפר, הזרם נטו הסגור בלולאה הוא אפס. במקרה של microstrip הזרם חוזר דרך המוליך החיצוני, שהוא ההארקה, מאחר שבחיבור פרמטר S הזרם חוזר דרך ההארקה. הגדרה זו בעייתית. למשל, במקרה של זוג חוטים הפרשי הפועל במצב הפרשי (איור 7), הזרם בשניהם שווה והפוך בכיוונו, לכן הזרם I הוא אפס והעכבה אינסופית. בדרך כלל מתייחסים למתח שבין הקווים ואז הגדרת העכבה היא:
המתח הוא אינטגרל השדה החשמלי לאורך מסלול. אם שני הקצוות הם המוליכים של ההארקה ושל האות, נפתרת בעיית העכבה. את קו כיול המתח אפשר להעביר מהצד של מוליך הגלים אל קו האות החיובי, או בין שני קווי האותות (איור 7).
מדמי שיטת המומנט וחיבורי port
באיור 8 מוצג כיפוף בקו microstrip. המוליך משולב לסדרת מלבנים או משולשים שאותם אפשר לסדר בצורה טובה יותר סביב קווים מעוקלים. הזרם מקורב בכל רשת באמצעות פונקציה פשוטה. ההנחה היא שהזרם משתנה באופן ליניארי מקצה לקצה.
הזרמים משתנים באופן משטחי. לאורך הקו קיימים מטענים חיוביים ושליליים. הזרמים והמטענים פועלים ביניהם. בין שני מטענים קיים קיבול ובין שני זרמים קיימת השראות. לכל זרם יש השראות ביחס להארקה ולכל מטען יש קיבול ביחס להארקה, והיא המשטח התחתון של קו microstrip.
חיבור port מזריק זרם למדמה EM. באיור 9 מתואר חיבור קצה (Edge Port) שאותו אפשר לראות כמקור מתח בטור לעכבה, שמזריק לקו. שים לב לעין הרשת הצרה לאורך קצה הקו, הנקראת רישות קצה(Edge Meshing). על פי מה שהתברר במשך השנים, היא מדויקת ויעילה ליצירת מודלים של קווים, מאחר שהזרם מתרכז בקצות הקו. במעגל השקול באיור 9, מתוארת ההארקה לחיבור קצה שמקומה עבור מדמה EM תלוי בפרטי החיבור.
סוג מדמי MoM אחד הוא מדמים בתיבה כמו EMSight או Sonnet. איור 10 מראה חיבור קצה שעבר כיול. השפעות המדידה בוטלו (de–embed) עבור החיבור בתיבה, כפי שמראה החץ. מישור הייחוס נמצא בקצה החץ. מקור המתח מחובר על פני מרווח קטן בדופן הצד של התיבה וזרם מוזרק לקו.
סוג שני הוא מדמים ללא תיבה, למשל AXIEM, Momentum או IE3D. מיקום ההארקה לחיבור זה אינו ברור מאליו והוא תלוי במימוש בתוכנה. אם משתמשים בחיבור הארקה מרומז, ההארקה נמצאת באינסוף. מאחר שמשטח האדמה הוא מוליך מושלם, אין על פניו הפרש מתחים.
איור 11 מציג חיבור קצה מחובר ביריעת זרם למישור ההארקה התחתון, אשר ממנו מגיע הזרם.
לסיכום, מדמי MoM תומכים במגוון חיבורים, לכל אחד הגדרת הארקה משלו. הדרך הקלה להתייחס להארקה היא להניח שהזרם היוצא מהחיבור למעגל מגיע מהארקת החיבור.
קווים דיפרנציאליים ו – Coplanar ports
שימוש רב נעשה בקווים דיפרנציאליים, הן לצרכי הזנת הספק RF, והן לשימושים דיגיטליים הדורשים אנליזת Signal Integrity. זכרו כי האדמה עבור המקרה של שני ports הינו באינסוף. במקרה הדיפרנציאלי, הזרם החיובי נע מה – port הראשון ויוצא מה – port השני.
קווים דיפרנציאליים שימושיים בעיקר לצרכי הקטנת רעשים, ונעשה בהם שימוש פופולארי באותות בעלי הספקים נמוכים. הרעיון העומד בבסיס השימוש בקווים דיפרנציאליים הוא שהתהליך המתרחש בקו אחד זהה לתהליך המתרחש בקו השני. כל קו מתייחס לקו השני כאל האדמה שלו. האופן הדיפרנציאלי מיושם ב – MWO (הסימולאטור הסכמאטי) באמצעות הזרקת שני Ports בעלי פולאריות הפוכה. הדבר מודגם באיור 12, שם נעשה שימוש בבלוק MMCONV (Mixed Mode Converter), המסייע ביצירה פשוטה של אות דיפרנציאלי.
קווי Coplanar כוללים קו המעביר אות ובנוסף שני משטחי אדמה מסביב. איור 13 מדגים מבנה א”מ בעל שש Edge ports. כאמור לעיל, האדמה של כל ה – ports נמצאת באינסוף. המבנה הספציפי אינו מכיל שכבת אדמה תחתיו. לכאורה, נראה שאין מסלול שדרכו יכול לעבור הזרם החוזר מהאינסוף אל ה – Port, שלא כמו המקרה של קו ה – Microstrip אשר היה צמוד עם האדמה המוגדרת היטב. עם זאת, כאשר ה – ports מוגדרים היטב ב – schematics, ניתן בהחלט לעורר את האופנים המשותפים, כמו גם את האופנים האי זוגיים (odd mode) הלא רצויים ואת אופני הקרינה. האופנים המשותפים באינסוף מתבטלים, דבר המוביל לתוצאות הרצה מדויקות, ללא צורך בשכבת אדמה מעל או מתחת למבנה ה – Coplanar. דבר זה לא היה אפשרי אם ה – port היה מחייב קישור אל שכבת אדמה כזו או אחרת בשכבה עליונה או תחתונה.
לסיכום, מדמי MoM תומכים במגוון חיבורים, לכל אחד הגדרת הארקה משלו. הדרך הקלה להתייחס להארקה היא להניח שהזרם היוצא מהחיבור למעגל מגיע מהארקת החיבור.
סיכום
הבנת ההארקה מאפשרת ליצור מודל של קווי תמסורת לביצוע הדמיה שלהם. בשימוש בפרמטרי S מניחים שקיימת הארקה משותפת לחיבורים, לפחות אם משתמשים בהם במדמה מעגלים. כדי להבין את ההארקה במדמי EM, יש להתחיל בחיבורי port, לכולם יש סוג כלשהו של תפישת הארקה. ראוי להבין מאין מגיע הזרם העובר בתוך החיבור. מדמים תלת–ממדיים משתמשים בגישה זו לחישוב עכבת החיבור. מדמי שיטת המומנט מעוררים חיבורים ממקור מתח שחייב להיות מחובר להארקה. כלי AXIEM הייחודי של AWR הוא בחירה טובה לסוגי יישומים אלו מאחר שהוא מספק גמישות בהגדרת מקום הארקת הייחוס.