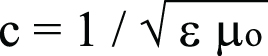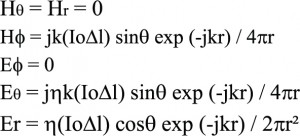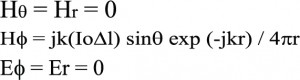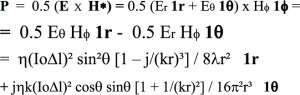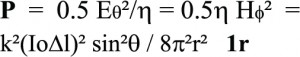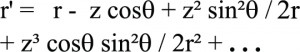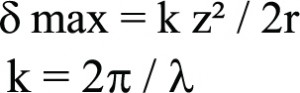פרופ’ עלי לוין, מכללת אפקה להנדסה, תל אביב
פרופ’ עלי לוין, מכללת אפקה להנדסה, תל אביב
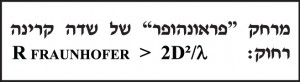
אחד המושגים הבסיסיים בתורת הגלים האלקטרומגנטיים הוא וקטור פוינטינג Poynting המציג את כיוון ההתפשטות של האנרגיה במרחב. המרחק שבו לוקטור פוינטינג יש משמעות ברורה הוא איזור הקרינה הרחוק הקרוי על שם פראונהופר Fraunhofer ואיזור הקרינה הקרוב הקרוי על שם פרנל Fresnel. במאמר זה נתאר את הקשר בין וקטור פוינטינג לבין איזורי פראונהופר ופרנל, תוך ציון הביוגרפיה של שלושת האישים המפורסמים האלו ופועלם המדעי.
1. הקדמה: גל אלקטרומגנטי המתפשט בחלל החופשי מוגדר לפי וקטור השדה החשמלי E ווקטור השדה המגנטי H. במרחק רב ממקור הגלים, הקרינה הופכת לגל מישורי planar wave שבו השדה החשמלי הוא רכיב יחיד (נניח E) והשדה המגנטי גם הוא רכיב יחיד הניצב לשדה החשמלי (נניח H). במקרה כזה קיטוב הגל המתפשט הוא לינארי לפי כיוון השדה החשמלי. היחס בין השדה החשמלי לבין השדה המגנטי מוגדר היטב וערכו:
(1)
c = מהירות האור
פרימיטיביות של הריק![]()
(3)
![]()
היחידות של השדה החשמלי הן
[Volt/meter] והיחידות של השדה המגנטי הן
[Ampere/meter] לכן היחידות של E/Hהן [Volt/Ampere] = [Ohm] כלומר:
(4)
![]()
כאשר הוא אימפדנס הגלים בריק.
במקום שבו קיימים הוקטורים של השדה החשמלי ושל השדה המגנטי ניתן להגדיר וקטור שלישי על ידי מכפלה וקטורית ביניהם. זהו וקטור פוינטינג על שם המדען האנגלי (John Henry Poynting (1852-1914 ולא במשמעות של הכוונה pointing כפי שרבים נוטים לטעות.
(5) S = E x H
אם וקטורי השדות האלקטרומגנטיים הופכים לרכיבים, למשל 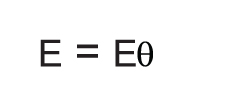 ,
, 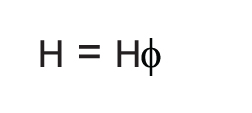 אזי וקטור פוינטינג יהפוך גם הוא לרכיב בודד בכיוון r
אזי וקטור פוינטינג יהפוך גם הוא לרכיב בודד בכיוון r
(6) Sr = E x H
והיחידות שלו תהיינה:
[Volt Ampere / m²] = [Watt / m²] כלומר הוא מבטא צפיפות קרינה או הספק ליחידת שטח. החלק הממשי של וקטור פוינטינג כפול 1/2 מבטא את ההספק הממוצע ליחידת שטח
(7)
האינטגרל המשטחי על וקטור פוינטינג מבטא את סך זרימת ההספק במרחב ואילו האינטגרל הנפחי מבטא את סך האנרגיה האגורה בחלל הנתון. משפט פוינטינג הוא תוצאה ידועה של משוואות מכסוול, המראה את סך ההספק הזורם דרך משטח או סך האנרגיה האגורה במרחב. בשתי הצורות הוא מבטא את חוק שימור האנרגיה האלקטרומגנטית.
נסכם אפוא:
במרחק רב מן המקור, הגל האלקטרומגנטי הוא מישורי וכולל רק את שני הרכיבים ![]() (במקרה הפרטי של קיטוב לינארי)
(במקרה הפרטי של קיטוב לינארי)
שני הרכיבים ניצבים זה לזה באופן מושלם
היחס ביניהם הוא אימפדנס הגלים בריק ![]()
המכפלה ביניהם היא וקטור פוינטינג
S = E x H המכוון לכיוון r
הערך ![]() מבטא את ההספק הממשי של הגל ליחידת שטח המועבר באוויר על ידי וקטור פוינטינג
מבטא את ההספק הממשי של הגל ליחידת שטח המועבר באוויר על ידי וקטור פוינטינג
כל אחד מן השדות דועך לפי ![]() ולכן וקטור פוינטינג דועך לפי
ולכן וקטור פוינטינג דועך לפי![]()
2. שדות הקרינה של מקור זרם אלמנטרי
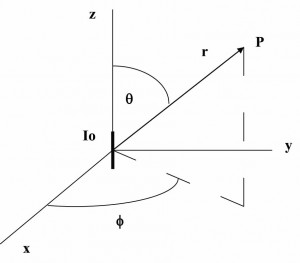
כדי לתאר את השדות האלקטרומגנטיים במרחב ביתר פירוט, מקובל להשתמש במודל פשוט יחסית של מקור זרם אלמנטרי כמתואר באיור 1. כאן מקור הזרם הוא חוט דק באורך ![]() הנושא זרם Io בכיוון z ואילו נקודת התצפית P נמצאת במרחק r מן הראשית השדות המגנטיים הנוצרים על ידי אלמנט הזרם הם:
הנושא זרם Io בכיוון z ואילו נקודת התצפית P נמצאת במרחק r מן הראשית השדות המגנטיים הנוצרים על ידי אלמנט הזרם הם:
השדות החשמליים הנוצרים על ידי אלמנט הזרם הם:
כשמתרחקים מספיק ממקור הזרם, איברים בחזקות גבוהות של דועכים והשדות העיקריים הנותרים הם בחזקת בלבד. בקירוב הידוע כמרחק פרנל ע”ש המהנדס הצרפתי Augustin Jean Fresnel מתקיים התנאי kr > 1 ושדות הקרינה הנותרים הם:
בקירוב פראונהופר ע”ש האופטיקאי הגרמני הידוע Joseph Von Fraunhofer מתקיים התנאי kr >> 1 ושדות הקרינה הנותרים הם:
(11)
כעת נוכל להתבונן בוקטור פוינטינג לפי השדות השונים המרכיבים אותו:
(12)
ובייחוד נמצא כי באיזור פראונהופר וקטור פוינטינג מתכנס לביטוי פשוט בהרבה:
(13)
ניתן לסכם אפוא כי באיזור פראונהופר שדות הקרינה הבלעדיים הם (או אם הקיטוב שונה אזי רכיבי השדה הרלבנטיים בהתאמה) אשר תלויים בחזקת בלבד ואז וקטור פוינטינג מופנה באופן בלעדי לכיוון ההתפשטות r וערכו תלוי בחזקת ![]() בלבד.
בלבד.
3. קירובי השדה לפי פראונהופר ולפי פרנל
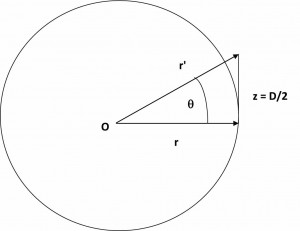
נציג עתה את קירובי השדה הרחוק על פי פראונהופר ועל פי פרנל כתוצאה של שגיאת פאזה מותרת על פני האנטנה. נתאר מקור קרינה בנקודה O המפזר את הקרינה עד למרחק r על פני גזרה בגודל 2z כמודגם באיור 2.
מרכז הגזרה נמצא במרחק r מן המקור ואילו קצה הגזרה נמצא במרחק ![]() מן המקור. זווית הראייה של הגזרה היא ולכן נוכל לרשום לפי משפט הקוסינוסים:
מן המקור. זווית הראייה של הגזרה היא ולכן נוכל לרשום לפי משפט הקוסינוסים:
ולפתח את השורש לטור אינסופי
כעת נזניח את האיברים הגבוהים ונתייחס רק לאיבר השלישי בסדרה כאל איבר השגיאה העיקרי. נניח שזווית ההסתכלות המכסימלית היא כך שהשגיאה המכסימלית היא z² / 2r. אם הגל האלקטרומגנטי פוגע באנטנה בגודל D המונחת בדיוק על הגזרה הנדונה (D = 2z) אזי שגיאת הפאזה הנוצרת בקצה האנטנה (ביחס למרכז האנטנה) תהיה:
קריטריון פראונהופר קובע כי שגיאת הפאזה המכסימלית על פני האנטנה, הנובעת מן האיבר השלישי תהיה ,
![]()
כלומר
ומכאן נובע שהמרחק r שבו מתקבלת שגיאת פאזה זו על פני האנטנה שגודלה D:
קריטריון פרנל קובע כי שגיאת הפאזה המכסימלית על פני האנטנה, הנובעת מן האיבר הרביעי תהיה ![]() וכדי לחשב אותה צריך קודם כל למצוא את זווית הראייה שבה השגיאה היא מכסימלית. נסמן את השגיאה e ונגזור אותה לפי
וכדי לחשב אותה צריך קודם כל למצוא את זווית הראייה שבה השגיאה היא מכסימלית. נסמן את השגיאה e ונגזור אותה לפי
הזווית שבה הנגזרת מתאפסת היא
![]()
arctan ואז תנאי פרנל הוא:
הצבה מתאימה של הזווית נותנת
כלומר, איזור פראונהופר שבו חזית הגל היא כמעט מישורית (עד כדי שגיאת פאזה של ![]() בקצות האנטנה) מוגדר לפי:
בקצות האנטנה) מוגדר לפי:
ואילו איזור פרנל שבו קיימת אלומת קרינה ראשית תקינה אך חזית הגל אינה בהכרח מישורית ואונות הצד עדיין אינן מדויקות מוגדר לפי:
בשני המקרים חייבים להניח ![]() וגם
וגם ![]() . המעבר מאיזור פרנל לאיזור פראונהופר אינו חד אלא הוא הדרגתי. כמו כן יש להעיר כי מדידת אנטנות באיזור פראונהופר אינה מבטיחה דיוק מוחלט. במקרים בהם מעונינים ברמת דיוק גבוהה במיוחד רצוי, במידת האפשר, להתרחק עד כדי
. המעבר מאיזור פרנל לאיזור פראונהופר אינו חד אלא הוא הדרגתי. כמו כן יש להעיר כי מדידת אנטנות באיזור פראונהופר אינה מבטיחה דיוק מוחלט. במקרים בהם מעונינים ברמת דיוק גבוהה במיוחד רצוי, במידת האפשר, להתרחק עד כדי ![]() ואף למעלה מזה.
ואף למעלה מזה.
4. הביוגרפיה של ג’ון הנרי פוינטינג
ג’ון הנרי פוינטינג נולד בשנת 1852 ונפטר בשנת 1914. הוא פעל באנגליה באוניברסיטת בירמינגהם, שם כיהן כפרופסור לפיזיקה משנת 1880. בשנים 1872 עד 1876 למד באוניברסיטת קיימברידג’ ואף זכה לעבוד במעבדת קוונדיש במחיצתו של ג’ימס קלרק מכסוול. פוינטינג עסק בתורת האלקטרומגנטיות, המציא את וקטור פוינטינג המצביע על כיוון זרימת ההספק וניסח את משפט פוינטינג המבטא את שימור האנרגיה בגלים אלקטרומגנטיים. בשנת 1903 פירסם עם רוברטסון את העובדה שקרינת השמש ניתנת להצגה כזרם חלקיקים וכן עסק במדידת קבוע הגרביטציה העולמי. ביחד עם תומסון כתב ספר לימוד רחב היקף בפיזיקה ששימש כספר הלימוד העיקרי באירופה במשך למעלה מ-50 שנה. מכתשים בירח ובכוכב מאדים נקראים על שמו.
5. הביוגרפיה של ג’וזף פון פראונהופר
ג’וזף פון פראונהופר נולד בשנת 1787 ונפטר בשנת 1826 בהיותו בן 39 שנים. פראונהופר חי ופעל בגרמניה בתחום המיכשור האופטי. פרסומו העיקרי נבע מגילוי פסי הבליעה בספקטרום של אור השמש (כ-576 קווי פראונהופר). בתאריך 21 ביולי 1801 נלכד בהתמוטטות בנין גדול וניצל בנס על ידי נסיך בוואריה בכבודו ובעצמו שאף העניק לו סכום כסף נאה לכבוד הצלתו. פראונהופר הצעיר השתמש בפרס כדי להשתלם בייצור עדשות במנזר בנדיקטוס במינכן. במהרה גילה יכולת טכנית נדירה והפך את המוסד הצנוע לתעשיה האופטית הטובה בעולם. פראונהופר היה אדם מעשי מאד והצליח לבנות מכשירים אופטיים איכותיים במיוחד – עדשות, מינסרות, טלסקופים, ספקטרומטרים ועוד – שזכו כולם להכרה עולמית. הוא לא פירסם ברבים את סודותיו המקצועיים ונהוג לטעון כי הם מעולם לא נתגלו ונקברו יחד איתו. על אף כישוריו הטכניים הנדירים הוא לא נחשב בזמנו לאיש מדע מובהק. ניתנה לו הרשות להשתתף באסיפות מדעיות אך לא לשאת בהן הרצאות.
6. הביוגרפיה של אוגוסטין ז’אן פרנל
אוגוסטין ז’אן פרנל נולד בשנת 1788 ונפטר משחפת בשנת 1827 בהיותו בן 39 שנים. פרנל חי ופעל בצרפת בתחום ההנדסה האופטית – הן בהיבטים עיוניים והן בהיבטים מעשיים. הוא המציא את העדשה השטוחה הנקראת על שמו בהיותו ממונה על רשת המגדלורים בצרפת. פרנל עסק בעיקר בתופעות העקיפה וההתאבכות, בהמשך ישיר לעבודותיהם של יאנג על האופטיקה הפיזיקלית והויגנס על ההתאבכות ממקורות רציפים. שני המאמרים הבולטים שפירסם הם:
Memoir on the diffraction of light (1812)
On the action of rays of polarized light upon each other (1819)
כמו כן תרם להבנת תופעות החזרה מפינות חדות ועל שמו נקראות תופעות עקיפה בגלי רדיו (מרחקי פרנל).
7. מראי מקום
[1] D. K. Cheng, Field and Wave Electromagnetics, Addison Wesley, 1989.
[2] H.A. Haus and J.R. Melcher, Electromagnetic Fields and Energy, Prentice Hall, 1989.
[3] W.L. Stutzman and G.A. Thiele, Antenna Theory and Design, John Wiley, second edition, 1998.
[4] J.D. Jackson, Classical Electrodynamics, John Wiley, third edition, 1998.
[5] D. J. Griffiths, Introduction to Electromagnetics, third edition, Prentice Hall, 1999.
[6] J. D. Kraus and R.J. Marhefka, Antennas for all Applications, McGraw Hill, third edition, 2002.
[7] R.S. Elliott, Antenna Theory and Design, John Wiley, 2003.
[8] C.A. Balanis, Antenna Theory Analysis and Design, Wiley Interscience, third edition, 2005.
[9] W.H. Hyat, Engineering Electromagnetics, McGraw Hill, 2005.
[10] F.T. Ulaby, Fundamentals of Applied Electromagnetics, Prentice Hall, 2010.
[11] J.A. Stratton, Electromagnetic Theory, Swedenborg, 2010.
[12] B. Thide, Electromagnetic Field Theory, www.plasma.uu.se, 2011.
פרופ’ עלי לוין הוא מרצה בכיר לתקשורת ולאנטנות באפקה, המכללה האקדמית להנדסה בתל אביב. בעלים ומנהל בחברת שדות וגלים בע”מ, העוסקת בהנדסת אנטנות ובשכבה הפיזית של מערכות אלחוטיות.
לתגובות: levineel@zahav.net.il