אבל עדיין יש לדעת כיצד לבחור את הגירוסקופ הנכון!
יש להזכיר כי הגירוסקופים משמשים ליישומי גילוי הסיבוב וניתן לכנותם גם חיישני מהירות זוויתית. הם מודדים את המהירות הזוויתית (הידועה גם תחת השם כוח קוריוליס) לאמור המהירות בה חפץ מסתובב. עבור הגירוסקופים בעלי יציאה אנלוגית, הסיבוב נמדד בדרך כלל במעלות לשנייה של שינוי ובהתייחס לשלושה צירים עלרוד (Y), סבסוב (Z), וגלגול (X)
במערכות הניווט, היציאה מהמהירות הזוויתי של גירוסקופ עוברת אינטגרציה כדי לקבוע את הכיוון הזוויתי אשר משמש לקביעת מידת סיבוב המערכת. כאשר משלבים בין זה לבין המידע על התזוזה, ניתן לקבוע את מיקומה. כאשר מתחילים לבחון גירוסקופ בעל ביצועים גבוהים, נהוג בדרך כלל להתחשב ביציבות ההתחלתית הטיפוסית של הגירוסקופ (באנגלית in run bias stability).
היציבות המפורטת היא בהגדרה סטנדרדית של התעשייה ערך תיאורטי או טוב יותר, דבר המניח תנאים אידיאלים. יחד עם זאת הגירוסקופים פועלים ביישומים ממשיים מחוץ למעבדה, ויש לקחת בחשבון את השפעת הסביבה. באופן אידיאלי, גירוסקופ יהיה רגיש למהירות הסיבוב בלבד. באופן מעשי, לכל הגירוסקופים יש רגישות מסוימת לתאוצה, בגלל האסימטריות של הארכיטקטורה המכאנית שלהם
ו/או לאי-דיוקים במיקרו-ייצור. למעשה, ניתן למצוא ביטויים רבים של רגישות לתאוצה, כאשר חומרתם משתנה מייצוב אחד למשנהו. החשובים ביותר הם בדרך כלל הרגישות לתאוצה ליניארית (המכונה רגישות G) ותיקון תנודות (רגישות g2).
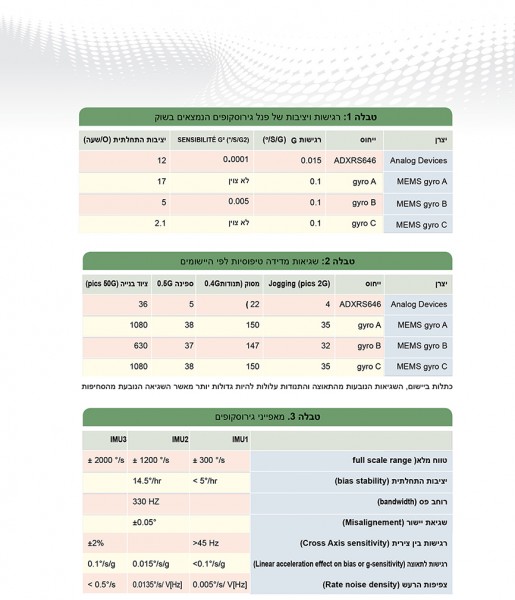
ההתקדמות האחרונה במיקרו-ייצור של גירוסקופים מאפשרת להם מעכשיו לפנות ליישומים בעלי הדרישות הגבוהות ביותר. מאחר שמרבית היישומים של הגירוסקופים הם אביזרים הנעים ו/או מסתובבים דרך שדה הכובד של כדור הארץ בכוח של 1G, הרגישות לתאוצה מהווה לעתים קרובות את מקור השגיאה העיקרי. טבלה 1 מראה את הספציפיקציות שנלקחו מהמפרטים הטכניים של מספר גירוסקופים MEMS בעלי ביצועים גבוהים. מרבית הגירוסקופים בקבוצה זאת מציגים רגישות G של
(דהינו ) ואחדים של פחות מ-. הרבה יותר טוב מאשר גירוסקופים מאוד זולים, אבל אפילו הטובים שביניהם עוברים על היציבות ההתחלתית המפורטת כאשר הם מתונים לתאוצה של 150 מ”ג (שוות ערך
להטיה של ° 8.6)
חישוב השגיאה הנובעת מתנודות ביישום נתון דורש ידע מסוים של גודל התאוצה הצפויה והתדירות בה היא מתרחשת. תנודות מסוק לדוגמה הם בדרך כלל די קבועות. מרבית הספציפיקציות הקשורות בתנודות של מסוקים הן בעלות ספקטרום רחב של 0.4 עבור מחזור עבודה של 100%. לצורך חישוב השגיאה הנובעת מתנודות אלה, יש לקחת בחשבון הן את הרגישות g והן את הרגישות g2. מכאן שעבור יישום על גבי מסוק, לדוגמה, השגיאות קשורות אחת בשנייה:
שגיאה = [שגיאת הרגישות g] + [שגיאת הרגישות g2]
שגיאה =
() +
אם הרגישות g מקוזזת על ידי מד תאוצה, אז רק הרגישות g מוקטנת על ידי מקדם הקיזוז. על ידי חישוב השגיאה על מספר חיישנים בטבלה 1, אנו מקבלים את התוצאות המוצגות בטבלה 2.
יישומי הגירוסקופ רגישים בו זמנית לתאוצה ליניארית, לתיקון התנודות ולסחיפות (in-run bias stability). יחד עם זאת, כפונקציה של היישום, השגיאות הנובעות מהתאוצה ו/או מהתנודות עלולות להיות גדולות יותר מאשר השגיאה הנובעת מהסחיפות Analog Devices הכניסה לאחרונה גירוסקופים עם ארבע מסות, אותם ניתן לכנות גם גירוסקופים עם ארבעה חיישנים. טכנולוגיה ייחודית זאת עם ארבעה חיישנים דיפרנציאליים, בהשוואה לגירוסקופים עם שני חיישנים השייכים למשפחות הקודמות, משפרת באופן משמעותי את תיקוני התנודות וקיזוז התאוצה הליניארית, כמו גם עמידות בזעזועים בטווח רחב מאות של תדירויות, דבר המאפשר מדידות אמינות ויציבות בסביבות קשות.
המצב העכשווי של גירוסקופים MEMS
הימצאות ארבעה חיישני מסה מספקת רמת סימטריה גבוהה, דבר יעיל מאוד נגד תנודות ותאוצה זוויתית. וזהו הציר העיקרי לפיתוח חיישנים גירוסקופים מרובעים: הם משפרים מאוד את הרגישות לתאוצה זוויתית (כאשר המהירות הזוויתית משתנה עם הזמן), בהשוואה לגירוסקופים בעלי שני חיישנים. שינוי זה מתורגם להקטנת התאוצה הזוויתית מ-0.2rad/s2 ל-0.006 rad/s2.
הגירוסקופים רגישים לכוח קוריוליס, שהוא אות חלש. האות יכול להיות מיוצג בערך על ידי מסה בתנועה היוצרת כוח; כך ניתן להגדיל את הכוח כך שיוכל להבחין טוב יותר ברעש. שני שיפורים עיקריים נבדקו בצורה זאת על ידי Analog Devices במטרה להגדיל את המהירות. מחד, יוצרים מרעידים את המסה בתנועה בתהודה הטבעית שלה על ידי הגברת המתח הדיפרנציאלי, דבר הגורם לתזוזה של המסה בתנועה מקדימה אחורה. היות והמסה הנעה רועדת כל הזמן בתדירות התהודה הטבעית שלה, “השעון” נוצר באופן מכאני (לא חשמלי). כל רכיב בתדירות השעון שלו. בדגמים החדישים יותר של גירוסקופים, תדירות התהודה של המסה הנעה היא בערך 14kHz ±3kHz. מאידך, המסה הנעה (המכונה גם רזונטור) זזה מקדימה אחורה בגלל הפרש המתחים בינה לבין מוטות ההפעלה של החיישן. השימוש במשאבת מטען מגביר את המתח, דבר המשפר את המהירות.
קיימות מספר טכניקות אחרות ידועות שלא הוטמעו במלואן בגירוסקופים העכשוויים, ושניתן עדיין להשתמש בהן כדי לשפר את הגירוסקופים MEMS בשנים הבאות. הרכיב חיישן מכאני ממוקם “בחדר אטום” וניתן ליצור ריק בחדר זה. מדובר בטכניקה בה נעשה שימוש בגירוסקופים MEMS חדישים של Analog Devices. הורדת הלחץ בתא מאפשר קיום מספר מצומצם של מולקולות במצע, דבר המשפר את המקדם Q של הרזונטור, וכתוצאה מכך מגביר את האמפליטודה שלהאות: וכך, מקדם Q גבוה מאפשר להקטין את רעש הכניסה (המבוטא ב-(). רעיון אחר הוא להגדיל את המבנים (על ידי הגדלת הצ’יפ המכאני) הדבר מתורגם ישירות להקטנת הרעש. ניתן להקטין את הרעש גם על ידי הגדלת עוביו של הפוליאימיד – תהליך הייצור של Analog Devices שונה כדי לעבור מעובי פוליאימיד של 2μm לעובי של 3μm ואחר כך 4μm. אריזה מבודדת זעזועים יכולה גם כן לסייע לשיפור הרגישות g ו-g2. (הדבר אינו נחוץ כאשר הרגישות g ו-g2 מצוינת, דבר המאפשר להציע פתרונות קטנים יותר וזולים יותר). ולבסוף, לכל הגירוסקופים יש רגישות מסוימת לתאוצה, בשל האסימטריות בתכנון המכאני שלהם
ו/או באי דיוקים במיקרו-ייצור. היצרנים לא בדקו עדיין את כל האפשרויות המוצעות על ידי מיקרו-ייצור שטח בדיוק גבוה. לכל הגירוסקופים MEMS יש שגיאה מסוימת של ממתח אפס ב-0=T, שגיאות מקדם קנה המידה, כמו גם שינויי טמפרטורה. בשל כך, מספר רב של פתרונות כוללות כבר כיול טמפרטורה מוטמע. קיימות טכניקות רבות בהן ניתן להשתמש לקיזוז הטמפרטורה. (התאמת עקומה הפולינומים, קירוב ליניארי בחלקים ועוד). יחד עם זאת, ללא קשר עם הטכנולוגיה המיושמת או תשומת הלב המושקעת, הגורם המגביל יהיה ההיסטרזיס התרמי – דהינו ההבדל ביציאה בטמפרטורה מסוימת, כאשר טמפרטורה זאת מושגת באמצעות קירור או חימום. אם היישום מאפשר להחזיר לאפס את ממתח אפס בזמן ההמראה (דהינו הנוצר כאשר אין סיבוב), או הורדה לאפס בזמן הפעלה של ממתח אפס, ניתן להתעלם משגיאה זאת. אם לא, הדבר עלול להגביל את ביצועיי היציבות, מפני
שלא ניתן לשלוט על תנאיי המשלוח או האחסון.
כל הטכניקות שנדונו לעיל מאפשרות לשפר את הטכנולוגיה של גירוסקופים MEMS, דבר המגביר את העניין בשימוש בהם ביישומים צבאיים/אוויריים. הגירוסקופים MEMS המשופרים הסדרה יכולים כיום להיות מוטמעים במערכות אינרציאליות בעלות ביצועים גבוהים. אבל יש עדיין צורך לדעת כיצד לבחון את מאפייניהם כדי שאפשר יהיה להשוות בצורה נכונה את השגיאות המורכבות שלהם.
לדוגמה ה- ו-2 בטבלה 3. התאוצה הליניארית או כאשר הרגישות g נתונה
ב-o/s/g: אנחנו משנה יחידה זאת ל-o/h/g, על ידי הכפלה ב-3600, שייתן 3600 עבור ה-IMU הראשון. אנו מניחים הטיה של 5O. כדי לתרגם זאת ל-g ניקח את הסינוס של 5O שהוא 0.0872
השגיאה הנגרמת על ידי ההטיה היא:
g x 360 °/h/g = 31,4 °/h .
השגיאה המשולבת היא השורש של הסכום בריבוע של 5O/h (היציבות ההתחלתית הטיפוסית) ושל 31.4O/h (השגיאה הנובעת מההטיה) מפני שמקורות שגיאה אלה אינם קשורים. השגיאה המשולבת היא:
(31,42 + 52) =/ 31,8°
אם לוקחים את ה-UMU השני (ADIS16488) ומפעילים עליו חישוב דומה מקבלים:
השגיאה בגלל ההטיה:
gx3,600 °/s x 0,015°/s/g = 4,7 °/h
14.5 היא היציבות הטיפוסית ההתחלתית של ADIS16488
השגיאה המשולבת היא:
V14,52 + 4,72 = 15,2°/h
לכן גם אם IMU גירוסקופ 1 מציע יציבות התחלתית טיפוסית של 5O/h, אם IMU זה נמצא במצב לא מושלם (לדוגמה הטיה מזערית של 5O ביחס לציר שלו) אזי הוא מתנהג כמו גירוסקופ/IMU של 31.8. הדבר ממחיש מדוע השגיאות הקשורות לסביבה הם באופן כללי מקור השגיאות העיקרי של הגירוסקופים.
ננקוט גישה אחרת בקשר לרעש הכללי של גירוסקופ, בהתייחסנו לרכיב אחר (שיכונה 3IMU), אותו נשווה מחדש ל-2IMU. השאלה הנשאלת כאן היא שהאם הסיבוב מתרחש רק סביב ציר Z (הציר האנכי) לדוגמה, אזי ניתן להניח כי באופן אידיאלי לא נצפה שום סיבוב סביב ציר X (אורך) וציר Y (רוחב) של הגירוסקופ; אבל אם הגירוסקופים עם ציר רוחבי או אורכי לא מיושרים בדיוק ב-90 ביחס לגירוסקופ עם ציר אנכי, אזי נראה את הסיבוב, אותו ניתן לחשב כסינוס של זווית הסטייה כפול מהירות הסיבוב.
לצורך הדוגמה שלנו נניח רוחב פס של 10Hz ובעל סיבוב של . תחילה יש להמיר את שגיאת הרגישות הבין צירית (Cross Axis sensitivity) על ידי הכפלתה במהירות הסיבוב אותה הנחנו:
שגיאה של:
0,02 x 30 °/s = 0,6 °/s
עבור 2IMU, מצוין חוסר היישור (Misalignement) ולא הרגישות הבין צירית: אנו נמיר את חוסר היישור לרגישות בין צירית על ידי גזירת הסינוס של הזווית: Sin 0,05° = 0,000873° או 0.0873%. חישוב דומה לחישוב הקודם נותן לנו שגיאת רגישות בין צירית:
0,000873 x 30°/s = 0,026°/s.
נחשב את הרעש RMS, הוא שווה ל:
צפיפות הרעש X (רוחב פס /2 x )
עבור 3 IMU:
רעש =V (π/2 x 10) x 0,005 = 0,0198°/sעבור 3 IMU:
רעש = π/2 x 10) x 0,01 = 0,0396°/s)
בהמשך, נגזור את השורש של סכום בריבועים של רעש RMS לעיל ורעש הרגישות הבין צירית, כדי לקל את השגיאה המורכבת.
שגיאה משולבת =
= (0,01982+0,62)
שגיאה משולבת 2 IMU =
V ( 0,03962 + 0,0262) = 0,0397°/s
כפי שראינו בדוגמאות אלה, מקורות השגיאה הקשורים בסביבה שולטות על הדיוק הכללי של החיישן.
הכותב פרנק פרונט (Analog Devices)
בעל דיפלומה של מהנדס מטעם בית הספר הגבוה להנדסת אלקטרוניקה ואלקטרו טכניקה של פריס, פרנק פרונט הצטרף ל-Analog Devices במאי 2011, כמהנדס יישומים עבור לקוחות צבאיים ואוויריים. קודם לכן הוא שימש כמהנדס יישומים על ה-FPGA של אלטרה במשך 10 שנים, אחרי שמילא תפקיד של מפתח ASIC/FPGA בעמק הסיליקון בתחילת הקריירה שלו.