קלוד שנון – מייסד תורת המידע

פרופ’ עלי לוין, מכללת אפקה להנדסה, תל אביב

קלוד שנון, מהנדס חשמל ומתמטיקאי אמריקאי (1916-2001) נחשב למייסד תורת המידע וכמי שהניח את היסודות המתימטיים המוצקים ביותר של התקשורת הספרתית. מיד עם פרסומו של מאמר מוביל בשנת 1948 הוכר כאחד המדענים המבריקים של המאה ה-20. מכל תרומותיו לעולם התקשורת בולט במיוחד הקשר הבסיסי בין קצב המידע, רוחב הסרט ויחס אות לרעש, הידוע כחסם שנון-הרטלי ונחשב לחוק המרכזי של תורת התקשורת. במאמר זה נסקור את הרקע ההיסטורי של תורת המידע, את תמצית קורות חייו של קלוד שנון ואת תרומתו הסגולית.

רקע היסטורי
תורת המידע לא נולדה ברגע מסוים אלא התפתחה באופן מתון יחסית בסוף המאה ה-19 ובמחצית הראשונה של המאה ה-20, בעיקר בארצות הברית אך גם במערב ובמזרח אירופה. במונח “מידע” information מתכוונים להעברת אותות ממקום למקום דרך תווך פיזי (ולא למונחים אחרים כגון knowledge או meaning הקשורים לתפיסה, לידיעה ולהבנה). תורת האינפורמציה היא אחד המאפיינים התרבותיים והחברתיים הבולטים של תקופתנו ולא בכדי יש סוציולוגים המכנים את העת החדשה בשם “עידן המידע” להבדיל מ”עידן הדפוס” או “העידן התעשייתי”. אין לתאר את חיינו הנוכחיים ללא רשת האינטרנט, הטלפון האלחוטי הנייד, הסיבים האופטיים, התקשורת והניווט הלוויניים, המדיה האלקטרונית, הסמרטפונים, הטבלטים והרשתות החברתיות. כולם נשענים על ההמצאות הראשוניות שפותחו במאה ה-19 ובהן מכשיר הטלגרף שפיתח סמואל מורס (1799-1872), הטלפון הקווי שפיתח אלכסנדר גרהם בל (1847-1922) והתקשורת האלחוטית המוקדמת שבנו היינריך הרץ (1857-1894), וג’וגליאלמו מרקוני (1874-1937).
התרומות המדעיות הבולטות במחצית הראשונה של המאה ה-20 היו עקרונות הדגימה – כלומר הפיכת אות רציף לסדרת אותות בדידים בהתאמה לתורת פורייה שניתח הארי ניקוויסט בשנות ה-20
[1-2] ותורת השידור והקליטה של אותות חשמליים שניסח ראלף הרטלי באותן שנים [3-4]. במקביל התפתחו טכנולוגיות המיתוג הספרתי ונבנו המחשבים הראשונים וכן התפתחו מכשירים להסתרת מידע על ידי הצפנה ומנגד מכשירים לשבירת הצפנים. האוסף המרשים של הרעיונות והטכנולוגיות לא היה מגובש עד להופעתו המטאורית של קלוד שנון, אשר ביולי ובאוקטובר של שנת 1948 פירסם בירחון הטכנולוגי של מעבדות בל מאמר מקיף במיוחד [5] ובו 77 עמודי תיאוריה עם 23 משפטים מתימטיים מוכחים ו-7 נספחים מפורטים. במאמר זה ובמאמר נוסף משנת 1949 [6] הוצגו הגדרות מפורטות ומדדים כמותיים של מידע והונח מבנה מתימטי אחיד ומדויק לקצב המידע ולכמות השגיאות המופיעות במעבר בין המקור והיעד. במרכזה של תורת התקשורת נוסח הקשר הבסיסי בין קצב המידע, רוחב הסרט ויחס אות לרעש הידוע כחסם שנון הרטלי.

הביוגרפיה של קלוד שנון
קלוד אלווד שנון Claude Elwood Shannon נולד בתאריך 30 באפריל 1916 ונפטר בתאריך 24 בפברואר 2001 בארצות הברית. שנון נולד בעיירה פטוצקי במישיגן וחי בילדותו בעיר גיילורד. הוא נודע בחיבתו היתרה לפרק ולהרכיב מכשירים חשמליים – מקלטי רדיו, מכשירי ניהוג לסירות, טלגרפים וכיו”ב. בהיותו תלמיד עבד כשליח בחברת התקשורת Western Union. בבגרותו למד באוניברסיטת מישיגן, בשנים 1932-1936 וסיים שם תואר כפול בהנדסת חשמל ובמתימטיקה. מיד לאחר מכן, בהיותו בן 20 החל ללמוד לתואר שני במכון הטכנולוגי של מסצ’וסט MIT והתמקד בבניית מערכות מיתוג עבור מחשבים אנלוגיים. הוא התעמק באלגברה הספרתית הידועה כאלגברה בוליאנית על שם ממציאה ג’ורג’ בול והוכיח כיצד ניתן להשתמש בעקרונותיה כדי לבנות מערכות מיתוג יעילות ופשוטות [7-8].
בשנת 1940 סיים את עבודת הדוקטורט שלו ב-MIT שעסקה במודלים מתימטיים של גנטיקה Algebra for Theoretical Genetics [] הוא החל ללמד במכון ללימודים מתקדמים בפרינסטון, שם פגש את ענקי הרוח של המאה ה-20 ובהם אלברט אינשטיין, קורט גדל, ג’ון פון ניומן, הרמן וייל ואחרים. מסופר שבאחת ההרצאות של שנון נכנס לאולם אלברט אינשטיין, שאל את הסטודנטים שישבו בשורות האחוריות דבר מה ונעלם. מיד לאחר ההרצאה מיהר שנון לברר מה שאל אלברט ונענה: הוא חיפש את השירותים.
המאמצים המדעיים והטכנולוגיים הכבירים שהושקעו במלחמת העולם השנייה משכו אותו להצטרף בשנת 1942 למעבדות Bell ולעסוק שם בפרויקטי תקשורת והצפנה מתקדמים. במעבדות Bell הכיר את אשתו המתימטיקאית אליזבט (בטי) והשניים נישאו בשנת 1949 וגידלו שלושה
ילדים, Robert James ,Andrew Moore Margarita Cathrine. במעבדות Bell השתתף בבניית מערכות הצפנה שהמפורסמת בהן היתה “טלפון X”, מערבל שיחות סודי שקישר בין וינסטון צ’רצ’יל בלונדון לבין תיאודור רוזוולט בוושינגטון ואיפשר להם לתאם את מהלכי המלחמה בדיסקרטיות מוחלטת. תקופה מסוימת עבד עם אלן טיורינג, מי שעמד בראש קבוצת המדענים האנגלית שפיצחה את מכונת הצופן הגרמנית אניגמה.
בשנים 1956 עד 1978 לימד קורסים מתקדמים בתקשורת ב-MIT ועסק במגוון נושאים הקשורים למיכשור אוטונומי, מערכות לומדות ותוכנות למשחק שחמט [10] והיה ידוע גם כלהטוטן חובב. קלוד שנון סיפר פעם בראיון עיתונאי כי הרעיונות העיקריים שלו לא הופיעו במקרה באמבטיה או מתחת לעץ אלא היו תוצאה של עבודה שיטתית ממושכת. לסיכום, קלוד שנון היה מדען פעיל ופורה במשך יותר מ-40 שנה אך הוא קנה את עולמו בזכות המאמר המונומנטלי שפורסם בשנת 1948 (בהיותו בן 32). קלוד שנון נחשב לאחד המדענים המבריקים והמשפיעים במאה ה-20 וזכה לפרסים ולתארי כבוד רבים. לתיאור מעמיק של פועלו הקוראים מופנים למראי מקום [11-12].

עיקרי תורת המידע
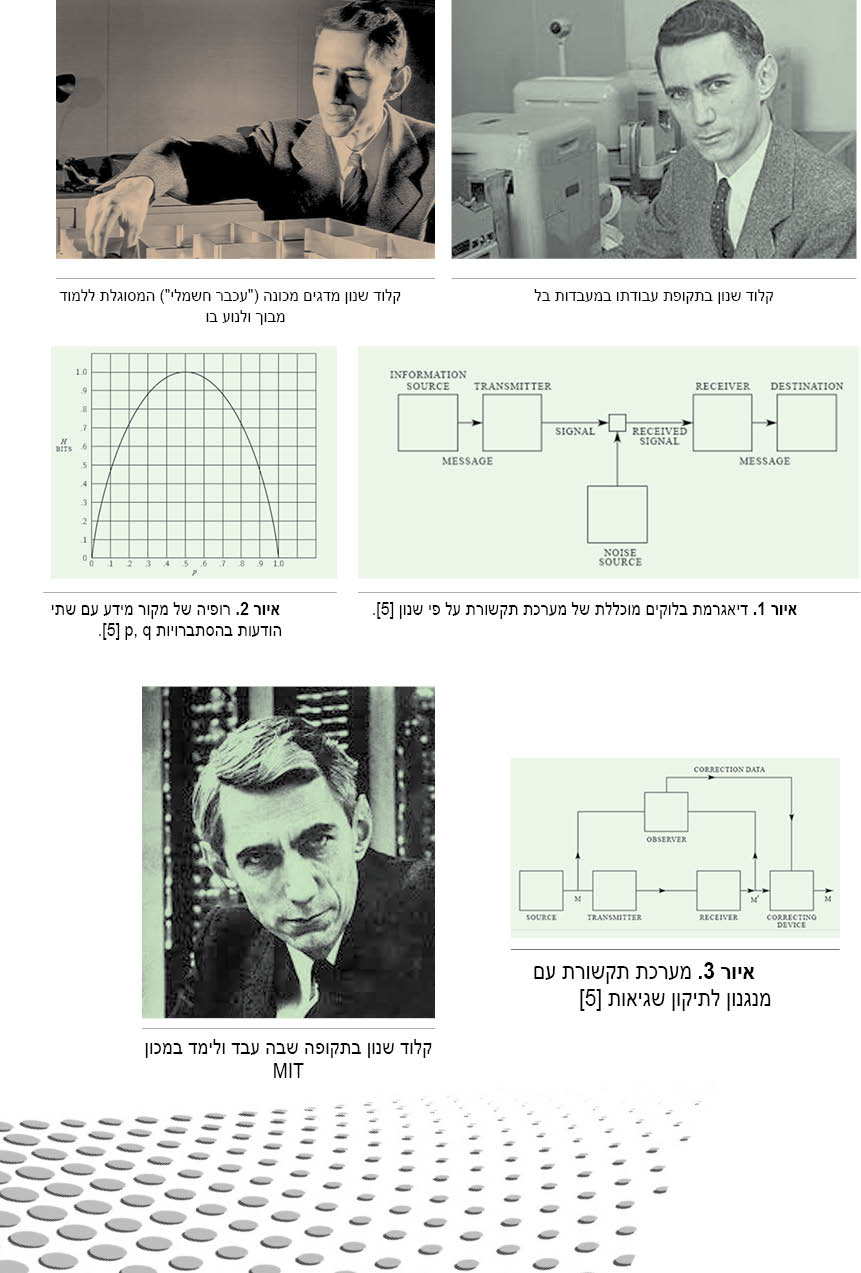
כל מערכת תקשורת נועדה להעביר הודעות ספציפיות ממקור המידע אל היעד באמצעות משדר ומקלט כאשר המידע עובר דרך תווך פיזי כלשהו ובתוספת מקור רעש הגורם לחלק מן ההודעות להגיע אל היעד עם שגיאות. איור 1 (מתוך המאמר המקורי של קלוד שנון) מדגים את דיאגרמת הבלוקים הבסיסית של כל מערכות התקשורת האלקטרוניות בעולם.
כמות המידע האגורה בהודעה כלשהי
נמצאת ביחס הפוך למידת ההסתברות המיוחסת להתרחשות ההודעה כלומר:

1)

הקשר המתימטי בין כמות המידע וההסתברות הוא פונקציית הלוגריתם, כאשר שנון בחר כבסיס הלוגריתם את המספר 2 כדי לבטא את המספר ביחידות דיגיטליות. כמות המידע כונתה bit במשמעות של binary digit. שנון טען כי הפונקציה הלוגריתמית היא היחידה שנמצאה מתאימה לתאר את הקשר הזה אך אין הוכחה שלא תיתכן פונקציה אחרת ולא מן הנמנע שבעתיד תימצא פונקציה נוספת.

2)

במקור מידע שיש בו N הודעות אפשריות, אגור מידע ממוצע שהתוחלת שלו היא:

3)

לתוחלת המידע האגור במקור ההודעות קרא שנון בשם אנטרופיה, באנלוגיה למושג האנטרופיה הידוע מן המכניקה הסטטיסטית והמבטא את רמת אי הסדר או את רמת חוסר הוודאות בצביר גדול של חלקיקים. ידוע כי קלוד שנון התלבט כיצד לכנות את תוחלת המידע האגור במקור והתייעץ עם הפיזיקאי הדגול ג’ון פון נוימן מאבות תורת הקוונטים. פון נוימן הציע לו את המונח אנטרופיה בהסבירו לשנון: “זה מונח מכובד שאף אחד לא באמת מבין אותו, כך שהוא יראה חשוב ומשמעותי”.
אם המקור כולל 2 הודעות בהסתברות p
ו-q=1-p (תמיד חייבים להראות כי סכום ההסתברויות של כל ההודעות שווה ל-1),
אזי האנטרופיה היא:
4)

ערכה של האנטרופיה בתלות בהסתברות p מתואר באיור 2 (גם הוא מתוך המאמר המקורי של שנון). אם p = q = 0.5 אזי האנטרופיה היא מכסימלית וניתן להבין זאת כאילו כמות אי הוודאות במקור היא מכסימלית. אם p >> q נוכל להבין כי רוב הזמן המקור פולט את ההודעה p ולא את q. לכן המקור מסודר יחסית. אם מגיעה הודעה כלשהי נוכל בהסתברות גבוהה לנחש כי היא מסוג p. בהכללה ניתן לומר כי כאשר מקור מידע כולל N הודעות האנטרופיה תהיה מכסימלית כאשר כל ההודעות שוות הסתברות p = 1/N וערכה יהיה .

5)

מקור המידע פולט הודעות (סימבולים) בקצב r סימבולים לשניה כאשר כל סימבול נושא בממוצע כמות מידע השווה לאנטרופיה H. היחידות של H הינן ביט לסימבול ואכן נשים לב כי בקידוד בינארי רגיל, עבור N = 2^n הודעות שונות, דרושים log2N ביטים כדי לרשום את כל ההודעות. מכאן קצב המידע הזורם מן המקור יהיה:

6)

עבור מקור מידע שבו ההודעות בהסתברויות שונות, הקידוד הבינארי אינו אופטימלי ומוצע קידוד אחר שבו הודעות שכיחות יירשמו על ידי מספר קטן של ביטים ואילו הודעות נדירות יירשמו על ידי מספר גדול של ביטים. שנון הציע, יחד עם דייויד פאנו, אלגוריתם אופטימלי לאריזת המידע על ידי הודעות בעלות אורך שונה וקרא לו “קידוד אנטרופי”. מספר שנים לאחר מכן הציע רוברט הפמן אלגוריתם שונה ובמשך שנים רבות ניטש ויכוח האם לאחד מן האלגוריתמים יש יתרון ביחס למשנהו. כיום ניתן להראות כי במקרים ספורים אכן האלגוריתם של הפמן יעיל יותר [13].
הדוגמה הקלאסית מן המאמר של שנון עוסקת במקור עם 4 הודעות
אשר הסתברותן, בסדר יורד הן
. אפשר להראות בעזרת משוואה (3) כי האנטרופיה היא H = 1.75. בקידוד בינארי רגיל נרשום את ההודעות בעזרת 2 ביטים לפי:
11 10 01 00 כלומר אורך המילה הממוצע יהיה L = 2 bit ולכן יעילות הקידוד תהיה . בקידוד אנטרופי המתקבל מאלגוריתם שנון-פאנו או מאלגוריתם הפמן נרשום את ההודעות לפי הסדר: 111 110 10 0 ולכן אורך המילה הממוצע יהיה L=1.75 bit ויעילות הקידוד תהיה 100%.
שנון ביקש לגלות מהו קצב המידע שניתן להעביר בערוץ תקשורת כלשהו בנוכחות רעש הגורם לשגיאות. הוא הניח כי הרעש הכללי ביותר הוא רעש תרמי אקראי מסוג AWGN = Additive White Gaussian Noise כלומר רעש שאינו תלוי סטטיסטית באות עצמו וניתן להוסיף אותו לאות, בעל ספקטרום תדרים אינסופי (כלומר באנלוגיה לאור לבן המורכב מכל אורכי הגל) ואשר צפיפות ההסתברות של המתח החשמלי היא פעמון גאוסי. ברור כי הרעש גורם לשגיאות בהעברת ההודעות אך אם המידע אינו רב מדי, אפשר לשדר בקצב איטי ובהספק גבוה כך שכמות השגיאות תהיה קטנה כרצוננו. בהסתמך על הנחת הרעש הגאוסי הלבן הוא מצא כי הספק הרעש המגיע למקלט הוא:

7)

k = Boltzmann Constant = 1.38 x 10^-23 [ Watt / K Hz]
T = Absolute Temperature of the receiver [K]
B = Bandwidth [Hz]

תוך שימוש במשפט הדגימה של נייקויסט ובתיאור המתימטי של הרעש הלבן, נמצא כי הערוץ מסוגל להעביר קצב מידע מכסימלי (“קיבולת הערוץ”) של C ביט לשניה השווה למכפלת רוחב הסרט של המקלט בלוגריתם של יחס אות לרעש.

8) C = B log2 (1 +SNR)
כאשר:
C = Capacity [bit per second]
B = Bandwidth [Hz = 1/second]
SNR = Signal to Noise Ratio = S/kTB [pure]

הקביעה הקטגורית והחשובה ביותר של שנון, הידועה כחסם שנון – הרטלי היא: בכל ערוץ תקשורת מכל סוג שהוא, קיימת קיבולת מידע מכסימלית C התלויה מצד אחד ברוחב פס התדרים של המקלט ומצד שני בלוגריתם יחס אות לרעש. הקצב המעשי R של המידע שניתן להעביר בערוץ, תוך הקטנת מספר השגיאות כרצוננו, תמיד יהיה קטן מן הקיבולת המכסימלית C.
9) R < B log2 (1 + SNR)

חסם שנון-הרטלי הוא כה יסודי עד כי הוא מיטיב לתאר ולדרג כל מערכת תקשורת שהיא. החסם מראה כי רוחב הסרט ויחס אות לרעש מאזנים זה את זה. אם דרוש לנו קצב מידע מסוים, נוכל להשיג אותו בין על ידי הגדלת B ובין על ידי הגדלת SNR. יחס R/B נקרא בדרך כלל בשם “יעילות ספקטרלית” ואילו הקשר בין SNR לבין כמות השגיאות בערוץ נקרא בדרך כלל בשם “יעילות הספק”. חסם שנון קושר אפוא בין היעילות הספקטרלית לבין יעילות ההספק ומראה את יחס החלופה ביניהם. במערכות מעשיות לא נוכל להשיג גם יעילות ספקטרלית גבוהה וגם יעילות הספק גבוהה ונצטרך לבחור ביניהן או להתפשר
על מצב ביניים. למשל ניתן לקבוע כי בערוץ שבו רוחב הסרט הוא MHz ויחס אות לרעש הוא SNR=10 dB = 10 קצב המידע המכסימלי
יהיה R = 20 x 3.5 = 70Mbps. באופן מעשי מערכות תקשורת פועלות מתחת לחסם שנון בהרבה.
אם B שואף לאינסוף הרי מקבלים:
10) lim R = B log2 (1 +S/kTB)
B
= (1/ln2) S/kT = 1.44 (S/kT)

ואם יחס אות לרעש שואף ל-1 (עדיין יש סיכוי לקלוט הודעות מפני ששני מצבי המקלט הם: רעש בלבד N או רעש ועוד אות S+N והיחס ביניהם הוא 2:1) הרי מקבלים:
11)

להשלמת הדיון נוסיף עוד כי שנון התעמק בטכניקות אפשריות לשיפור יעילות ההספק על ידי גילוי ותיקון שגיאות. גילוי ותיקון שגיאות אפשריים אם נוסיף למידע הנקי מעטפת של ביטים נוספים. למשל, אם במקום לשדר את המידע 001 נשדר אותו שלוש פעמים 001 001 001 נוכל לשפר את הקליטה. אם תופיע שגיאה אחת בדרך כגון 001 101 001 עדיין נוכל להסיק לפי עקרון הרוב מהו המידע הסביר שהיה צריך להגיע. כמובן ששידור כזה הוא בזבזני מאד (היעילות הספקטרלית קטנה פי 3 מהיעילות ללא איברי תיקון). יש אלגוריתמים מתוחכמים רבים כגון על שם ריצ’ארד המינג שבהם משיגים תיקון טוב במחיר זול בהרבה. קלוד שנון לא טרח לפרט כיצד ניתן לתקן את השגיאות אבל התווה את הדרך ואת התרומה הרבה של מנגנוני תיקון השגיאות לאיכות התקשורת שאפשר לקבל כמודגם באיור 3.
בשנים האחרונות התפתח מגוון רחב של מערכות תקשורת אלחוטיות הפועלות בתווך עם החזרות מרובות, הסתרות ופיזורים. בתווך כזה קיימת דעיכה אקראית חזקה של האותות והאותות המגיעים למקלט רוויים בהפרעות ועיוותים. אחת הדרכים המרכזיות להתמודדות עם בעיית הדעיכות בנתיב האלחוטי היא ריבוי אנטנות בשידור ובקליטה. בשיטה כזאת מייצרים באופן אפקטיבי מספר גדול יותר של ערוצים בין המקלט והמשדר ומגדילים את ההסתברות שלפחות חלק מן המידע יצליח לעבור כהלכה. במערכות אלו הנקראות MIMO = Multi Input Multi Output משיגים גם הגדלה משמעותית של היעילות הספקטרלית [14-15] הניתנת לניסוח כללי על ידי גירסה מודרנית של חסם שנון-הרטלי. ניתן להראות כי במערכת תקשורת מרובת אנטנות שבה M אנטנות שידור ו-N אנטנות קליטה, חסם שנון הרטלי ניתן לכתיבה על ידי:
12) R < min (M,N) x B log2 (1+SNR)

כלומר, כדאי מאד שמספר האנטנות במקלט ובמשדר יהיה זהה ואכן תצורותMIMO נפוצות במיוחד הן בגודל 2×2 או 4×4.
מראי מקום
[1] H. Nyquist, “Certain Factors Affecting Telegraph Speed”, Bell System Technical Journal, Vol. 3, p. 324, April 1924.
[2] H. Nyquist, “Certain Topics in Telegraph Transmission Theory”, Trans. AIEE, Vol. 47, pp. 617-644, April 1928.
[3] R.V.L. Hartley. “The Transmission of Information”, International Congress of Telegraphy and Telephony. Lake Como, Italy, September 1927.
[4] R.V.L. Hartley, “Transmission of Information”, Bell System Technical Journal, Vol. 3, pp 535-564, July 1928.
[5] C.E. Shannon. “A mathematical theory of communication”, Bell System Technical Journal, vol. 27, pp. 379–423 and 623-656, July and October 1948.
[6] C.E. Shannon, “Communication Theory of Secrecy Systems”, Bell System Technical Journal, Vol. 28, pp. 656–715. October 1949.
[7] C.E. Shannon, “A Symbolic Analysis of Relay and Switching Circuits,” unpublished MS Thesis, Massachusetts Institute of Technology, August 10, 1937.
[8] C.E. Shannon, “A Symbolic Analysis of Relay and Switching Circuits”. Trans. AIEE Vol..57,pp. 713-723. 1938.
[9] C.E. Shannon, “An Algebra for Theoretical Genetics”, MIT PhD Thesis, Department of Mathematics, 1940.
[10] C.E. Shannon, “Programming a Computer for Playing Chess”, Philosophical Magazine, Vol. 41, No. 314, March 1950.
[11] E. M. Guizzo, “The Essential Message: Claude Shannon and the Making of Information Theory”, M.S. Thesis, Massachusetts Institute of Technology, Dept. of Humanities, Program in Writing and Humanistic Studies, 2003.
[12] E. Chiu, J, Lin, B, Mcferron, N, Petigara and S. Seshasai, “Mathematical Theory of Claude Shannon”, The structure of Engineering Revolutions, web.mit.edu/6.933J/STS 4.20.
[13] A.B. Carlson, P.B. Crilly and J.C. Rutledge, Communication Systems, McGraw-Hill, Fourth Edition 2002.
[14] S. Barbarossa, Multiantenna Wireless Communication Systems. Artech House, 2005.
[15] A. El Zoogley, Smart Antenna Engineering, Artech House, 2005.
אמיר קליסמן, האב הלא נודע של תורת [16] המידע, גלילאו, עמודים 36-47, יוני 2.2008

לתגובות ElyL@afeka.ac.il