אף שבתיאורים רבים, האפנון מתואר כתהליך הכפלה, האמת מעט יותר מורכבת. ראשית, על מנת להבהיר זאת היטב, אם שתי הכניסות של מכפיל מושלם היו מוזנות עם אותAcos (ωt), ועם גל נושא לא מאופנןcos (ωt), התוצאה תהיה מאפנן. דבר זה קורה כיוון ששתי צורות הגל המחזוריות, Ascos(ωst) ו – Accos(ωct), המוכנסות לכניסות מכפיל (עם קנה מידה של 1 וולט, למען פשטות הניתוח), יוצרות יציאה הניתנת על ידי:
V0(t) = ½AsAc[cos((ωs + ωc)t) + cos(ωs – ωc)t))]
אם לגל הנושא Accos(ωct) יש משרעת של 1 וולט (1=AC), הדבר מפושט עוד ל:
V0(t) = ½As[cos((ωs + ωc)t) + cos((ωs – ωc)t)]
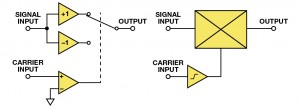
אך ברוב המקרים, מאפנן מהווה מעגל טוב יותר לביצוע פונקציה זו. מאפנן (הנקרא גם מערבל כאשר הוא משמש כמחליף תדר) מאד קשור למאפנן. תפוקת מכפיל היא המוצר המיידי של הכניסות שלו. תפוקת מאפנן היא המוצר המיידי של האות באחת מהכניסות שלו (הידוע כאות כניסה) וסימן האות בכניסה השנייה (הידועה ככניסת הגל הנושא). איור 1 מציג שתי דרכים לדיגום פונקציית האפנון: כמכפיל אשר ההגברה שלו ממותגת חיובית ושלילית על ידי יציאת מָשווֶה על כניסת הגל הנושא שלו, או כמכפיל עם מגבר מגביל הגברה גבוהה בין כניסת הגל הנושא ואחת מיציאותיו. שתי הארכיטקטורות שימשו ליצירת מאפננים, אך גרסת המגבר הממותג (המשמש במאפנן המאוזן AD630) נוטה להיות איטית יותר. רוב מאפנני מעגל משולב מהירות – גבוהה, כוללים מכפיל טראנסליניארי (מבוסס על תא גילברט) עם מגבר מגביל במסלול הגל הנושא המניע – ביֶתֶר את אחת הכניסות. מגבר מגביל זה עשוי לספק הגברה גבוהה, המאפשרת כניסת גל נושא ברמה – נמוכה, או הגברה נמוכה ומאפיינים מגבילים נקיים. וכך, עבור פעולה נכונה, הוא דורש כניסת גל נושא גדולה באופן יחסי. ראה את דף הנתונים למידע ספציפי.
איור 1. שתי דרכים לדיגום פונקציית האפנון
אנו משתמשים במאפננים ולא במכפילים, מכמה סיבות. שתי היציאות של המכפיל הינן ליניאריות, כך שכל רעש או אפנון על הגל הנושא מכפילים את אות הכניסה ומורידים את איכות היציאה, בעוד שלרוב, ניתן להתעלם משינוי המשרעת על הגל הנושא של המאפנן. מנגנונים משניים עלולים לגרום לכך שרעש המשרעת על הגל הנושא ישפיע על היציאה, אך הדבר ממוזער במאפננים הטובים ביותר והם לא יידונו כאן. דגם פשוט של מאפנן, משתמש במפסק המונע על ידי גל נושא. למפסק (מושלם) פתוח, יש התנגדות אין-סופית וזרם רעש תרמי אפס, למפסק (מושלם) סגור, יש אפס התנגדות ואפס מתח רעש תרמי, כך שמאפננים, אף שהמפסקים שלהם אינם מושלמים, נוטים להיות בעלי רעש פנימי קטן יותר ממכפילים. כמו כן, קל יותר לתכנן ולייצר מאפנן תדר-גבוה, רב-ביצועים, מאשר מכפיל בעל תכונות דומות. בדומה למכפילים אנלוגיים, מאפננים מכפילים שני אותות, אך שלא כמו מכפילים אנלוגיים, ההכפלה אינה ליניארית. במקום זאת, אות כניסה מוכפל על ידי +1, כאשר הקוטביות של הגל הנושא בכניסה הנה חיובית, ועל ידי -1, כאשר היא שלילית. במילים אחרות, האות מוכפל על ידי גל מרובע בתדר הגל נושא.
גל מרובע עם תדר של ωct עשוי להיות מיוצג על ידי סדרת פורייה של הרמוניקות לא-זוגיות:
K[cos(ωct) – 1/3cos(3ωct) + 1/5cos(5ωct) – 1/7cos(7ωct) + …]
סכום הסדרה[+1, -1/3, +1/5, -1/7 + …] הוא4 /π. לכן, הערך של K הוא 4/π, כך שמאפנן מאוזן פועל כמגבר בעל הגברה של יחידה כאשר אות ז”י חיובי מופעל על הגל הנושא שלו.
משרעת הגל הנושא אינה חשובה כל עוד היא גדולה מספיק על מנת להניע את המגבר המגביל, כך שמאפנן מונע על ידי אות – Ascos(ωst) וגל נושא – cos(ωct), יפיק יציאה אשר הנה המוצר של האות ושל הגל הנושא המרובע:
2As/π [cos(ωs + ωc)t + cos(ωs – ωc)t –
1/3{cos(ωs + 3ωc)t + cos(ωs – 3ωc)t} +
1/5{cos(ωs + 5ωc)t + cos(ωs – 5ωc)t} –
1/7{cos(ωs + 7ωc)t + cos(ωs – 7ωc)t} + …]
יציאה זו כוללת את התדירויות של הסכום ושל ההפרש של האות ושל הגל הנושא, ושל האות ושל כל אחת מההרמוניקות הלא – זוגיות של הגל הנושא. במאפנן אידיאלי מאוזן באופן מושלם, לא קיימים תוצרים של הרמוניקות זוגיות. אך במאפנן אמיתי, התוצאה של אופסֶטים שעוריים על יציאת הגל הנושא היא תוצרי הרמוניקות זוגיות, רמה-נמוכה. ביישומים רבים, מסנן מעביר נמוכים (LPF – low-pass filter) מסלק את התוצרים של ההרמוניקות הגבוהות.
זכור כי cos(A) = cos(-A), , כך ש – ωm)tcos(ωm – Nωc)t = cos(Nωc -, ולא נצטרך לדאוג מפני תדירויות “שליליות”. לאחר סינון, יציאת המאפנן ניתנת על ידי: 2As/π[cos(ωs + ωc)t + cos(ωs – ωc)t] זהו אותו ביטוי כמו היציאה של מגבר, אך עבור הגברה שונה מעט. במערכות מעשיות, ההגברה מנורמלת על ידי מגברים או מנחתים, כך שאנו לא נדון בהגברה התיאורטית של מערכות שונות כאן.
במקרים פשוטים, ברור שטוב יותר להשתמש במאפנן מאשר במגבר, אך השאלה היא כיצד אנו מגדירים ‘פשוט’? כאשר מאפנן משמש כמערבל, כניסות האות והגל הן גלי סינוס פשוטים בתדירויות f1 ו – fc, והיציאה הלא מסוננת כוללת את הסכום (fc + f1) וההפרש (fc – f1) פלוס תדירויות הסכום וההפרש של האות ושל ההרמוניקות הלא – זוגיות של הגל הנושא (f1 + 3fc), (f1 – 3fc), (f1 + 5fc), (f1 – 5fc), (f1 + 7fc), (f1 – 7fc).…. אחרי ה – LPF, אנו מצפים למצוא רק את התוצרים הבסיסיים, (fc + f1) ו – (fc – f1).
אך אם (fc + f1) > (f1 – 3fc), לא יהיה אפשר להפריד בין התוצרים הבסיסיים ושל ההרמוניקות עם מסנן LPF פשוט, כיוון שאחד התוצרים של ההרמוניקות נמצא בתדירות נמוכה יותר מאחד התוצרים הבסיסיים. זה אינו מקרה פשוט, לכן דרוש ניתוח נוסף.
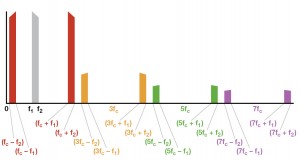
אם אנו מניחים כי האות כולל תדירות יחידה, f1, או אות מורכב יותר הפרוש על פני הפס מ – f1ל – 2f, אנו יכולים לנתח את ספקטרום היציאה של המאפנן שלנו, כפי שמוצג הדבר בתרשימים שלהלן. הנח מאפנן מאוזן באופן מושלם ללא זליגת אות, זליגת גל נושא או עיוות, כך שהכניסה, הגל הנושא, ותוצרים מלאכותיים, אינם מופיעים ביציאה. הכניסות מוצגות בשחור (או באפור בהיר בתרשימי היציאה, אף שהן אינן תמיד נוכחות).
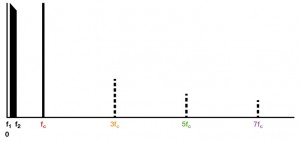
איור 2 מציג את הכניסות – אות בפס ה – f1ל – 2f וגל נושא ב- 2f. למכפיל לא יהיו הרמוניקות גל נושא לא – זוגיות ב – (3fc), 1/5(5fc), 1/7(7fc)1/3…, המוצגים כקוו מנוקד עבור המאפנן. שים לב כי השברים 1/3, 1/5, ו – 1/7 מתייחסים למשרעת, לא לתדירות.
ספקטרום הכניסה מציג את אות הכניסה, את הגל הנושא, ואת ההרמוניקות הלא –
זוגיות של הגל הנושא
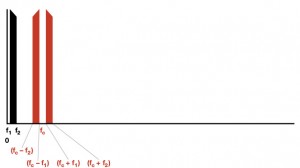
איור 3 מציג את יציאת המכפיל, או המאפנן, ו – LPF עם תדר קיטוע של 2fc.
איור 3. ספקטרום היציאה של מכפיל, או מאפנן, בתוספת LPF
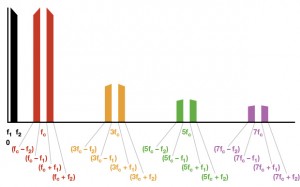
איור 4 מציג את היציאה של מאפנן לא – מסונן (אך לא תוצרי הרמוניקה מעל 7fc)
איור 4. ספקטרום היציאה של מאפנן לא – מסונן
אם פס האות, f1ל – 2f, נמצא בתוך פס ה – Nyquist(dc to fc/2), LPF עם קיטוע מעל 2fcיגרום לאותו ספקטרום יציאת מאפנן כמו זה של מכפיל. בתדירויות אות מעל Nyquist, הדברים הופכים למורכבים יותר.
איור 5 מציג את המתרחש כאשר פס האות נמצא בדיוק מתחת ל – fc. עדיין אפשר להפריד את תוצרי ההרמוניקה מאלו הנוצרים על ידי ההרמוניקות הבסיסיות, אך עתה נדרש LPF עם שיפוע מאד תלול.
איור 5. ספקטרום היציאה כאשר האות גדול מ – fc/2
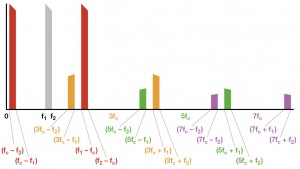
באיור 6, בעת שפס האות עובר דרך fc, התוצרים ההרמוניים עולים עתה אחד על השני,(3fc –f1) < (fc +f1) , כך שלא ניתן יותר להפריד את התוצרים הבסיסיים מהתוצרים ההרמוניים באמצעות LPF. עתה, יש צורך לבחור את האותות הנדרשים באמצעות מסנן מעביר פס (band-pass filter – BPF).
לכן, אף שמאפננים טובים יותר ממכפילים ליניאריים עבור רוב יישומי החלפת תדירויות, חשוב לשקול את תוצרי ההרמוניקות שלהם בעת תכנון מערכות אמתיות.
איור 6. ספקטרום היציאה כאשר האות גדול מ – fc
הפניות
Analog Dialogue
Brandon, David. “Multichannel DDS Enables Phase-Coherent FSK Modulation.” Analog Dialogue, Volume 44, Number 4, 2010.
Gilbert, Barrie. “Considering Multipliers (Part 1).” Analog Dialogue, Volume 42, Number 4, 2008.
המחבר הינו מנהל יישומים אירופאי ב-Analog Devices מאז 1982. בעל תואר בפיזיקה ובפילוסופיה מאונ’ לידס. כמו כן, הוא מהנדס בעל תארים C.Eng., Eur. Eng., MIEE, ו-FBIS.
