ניתוח אלקטרומגנטי עבור כבל קואקסיאלי בתדרים גבוהים

 

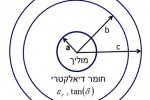
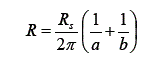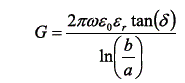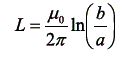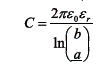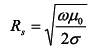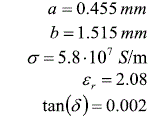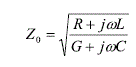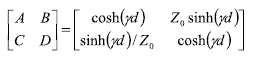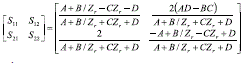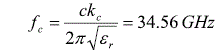כבל קואקסיאלי (coaxial cable) זהו כנראה הכבל הנפוץ ביותר ויחסית קל להבנה מבחינת ניתוח אלקטרומגנטי. כבלים קואקסיאלים משמשים להעברת אנרגיה או אותות, לדוגמא בין האנטנה לכניסה של המקלט. הכבל בנוי משני מוליכים המופרדים על ידי חומר דיאלקטרי, לצורכי בידוד, כפי שמוצג באיור 1. שני המוליכים מקבילים והציר המרכזי משותף לשניהם, לכן הכבל נקרא קואקסיאלי.

אחד היתרונות של הכבל קואקסיאלי, שניתן להשתמש בו מ-DC  ועד לתדרים גבוהים מאוד. בדרך כלל, רצוי לעבוד באופן (mode) הראשון, שהוא Transverse Electromagnetic , כאשר הרכיב של השדה החשמלי והשדה המגנטי שווים לאפס בכיוון התקדמות הגל (לאורך הכבל). כיוון השדה החשמלי, כיוון השדה המגנטי וכיוון התקדמות הגל מאונכים אחד לשני.

 

חישוב פרמטרים השקולים של קו תמסורת

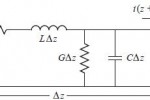
כאשר המימדים של קו תמסורת בסדר גודל של אורך גל או אורכי גל רבים, יש צורך להשתמש בתאוריה של קו תמסורת (transmission line). קו תמסורת TEM ניתן לתאר ע”י מודל מקובץ (lumped) שקול R, L, G, C, כפי שניתן לראות באיור 2.

עבור כבל קואקסיאלי, ניתן לחשב את הפרמטרים הנ”ל ע”י שימוש בנוסחאות הבאות:

התנגדות ליחידת אורך, עבור שני מוליכים (מייצג את ההתנגדות הסופית של שני המוליכים), .

מוליכות ליחידת אורך, (מייצג את ההפסדים הדיאלקטריים בחומר מבודד), S/m

 

השראות ליחידת אורך, (מייצג את ההשראות העצמית של שני המוליכים), H/m

 

 

קיבול ליחידת אורך, (מייצג את הקרבה בין שני המוליכים), F/m

התנגדות משטחית, – מוליכות של שני המוליכים

 

באופן כללי, כאשר מתכננים קו תמסורת מסויים, לדוגמא קו מיקרוסטריפ, סטריפליין וכו’, היתרון בתכנון הראשוני של קו תמסורת ע”י חישוב של הפרמטרים R, L, G, C בכך שניתן לחשב בנפרד פרמטרים שונים, כגון מקדם דעיכה בגלל הפסדים דיאלקטריים, מקדם דעיכה בגלל הפסדי מוליכות, איפדנס אופייני של קו תמסורת, מהירות התקדמות הגל וכו’. אם לדוגמא מקבלים מקדם דעיכה בגלל הפסדים דיאלקטריים גבוהה, אפשר לשקול להחליף את סוג החומר הדיאלקטרי ולבחור חומר עם הפסדים נמוכים יותר. ברוב המקרים, את הפרמטרים R, L, G, C נדרש לחשב ע”י חישובים נומריים, מפני שהפתרון האנליטי לא קיים או מאוד מסובך. מפני שעבור כבל קואקסיאלי קיים פתרון אנליטי עבור הפרמטרים R, L, G, C, אנו נראה השוואה בין החישוב האנליטי לחישוב הנומרי לצורך הדגמת הרעיון.

לדוגמא, נבחר את הפרמטרים הבאים של הכבל:

היחס בין הרדיוסים נבחר כך שהאימפדנס האופייני יהיה  (בהנחה שאין הפסדים בכבל), המחושב ע”י . שורש של L/C

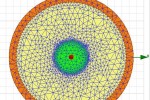
עבור החישוב הנומרי נעזרנו בתוכנה Q2D Extractor של ANSYS, במישור התדר, בשיטת  (Finite Element Method), כאשר החלוקה של Mesh היא לפי משולשים. לצורך החישוב של הפרמטרים R, L, G, C לא נדרש לדעת את האורך של הקו, אלא רק את החתך הרוחבי (ההנחה שהחתך הרוחבי קבוע לאורך הקו). באיור 3 ניתן לראות את החלוקה של Mesh בחתך הרוחבי של כבל קואקסיאלי בתוכנת Q2D Extractor.

עבור החישוב האנליטי קיבלנו C=96.21pF ו-L=240.53nH. עבור החישוב הנומרי קיבלנו C=96.22pF

ו-240.65nH < L < 240.95nH. הסיבה להבדל בהשראות ליחידת האורך היא בגלל שבחישוב הנומרי מתחשבים גם בהשראות הפנימית בתוך המוליכים. במודל השקול של קו תמסורת אנו מתחשבים בהשראות החיצונית בלבד ומזניחים את ההשראות הפנימית. הההשראות הכוללת הינה הסכום של השראות הפנימית והשראות החיצונית.

התוצאות עבור התנגדות ומוליכות ליחידת אורך מוצגות באיורים 4 ו – 5, בהתאמה. ניתן לראות שישנה התאמה כמעט מושלמת בין החישובים האנליטיים לנומריים.

חישוב S פרמטרים

לאחר שחישבנו את הפרמטרים R, L, G, C, נרצה לחשב את S  פרמטרים של קו תמסורת: מקדם החזרה (S11) ומקדם העברה (S21), זאת על מנת להבין מהם ההפסדים במערכת. לצורך חישוב זה, נדרש לדעת את האורך של קו תמסורת d, את אימפדנס המקור ואימפדנס העומס המחוברים לקו תמסורת. נניח שאימפדנס המקור ואימפדנס העומס זהים ונסמן

ב- Zr

עבור קו תמסורת עם הפסדים, מקדם התפשטות המרוכב, נתון ע”י:

כאשר  מקדם דעיכה ו- מקדם התפשטות.

אימפדנס האופייני, עבור קו תמסורת עם הפסדים מוגדר:

נוח לבצע חישוב בשני שלבים:

1. חישוב מטריצת ABCD בעזרת מקדם התפשטות המרוכב ואימפדנס האופייני של קו תמסורת:

2. חישוב מטריצת S מתוך מטריצת ABCD:

כאשר ישנו תיאום אימפדנסים מושלם , מקבלים

חישבנו את מקדם העברה (S21) ב-dB עבור כבל קואקסיאלי באורך 10mm עם הנתונים של הדוגמא הראשונה, כאשר החישוב נעשה עבור שלושת המקרים:

• הפסדי מוליכות
• הפסדים דיאלקטריים
• הפסדי מוליכות והפסדים דיאלקטריים

בנוסף לחישוב האנליטי וחישוב נומרי בתוכנת Q2D Extractor, השתמשנו בתוכנה תלת מימדית HFSS של ANSYS במישור התדר, בשיטת , כאשר החלוקה של Mesh היא לפי טטראדרים. באיור 6 ניתן לראות את המודל בתוכנת HFSS והתוצאות שהתקבלו מוצגות באיור 7. באיור זה ניתן לראות שישנה התאמה מאוד טובה בין שיטות חישוב שונות. ניתן להבין מהגרף מה התרומה של כל סוגי ההפסדים.

 

חישוב אופנים מסדר גבוהה

באופן כללי, בקו תמסורת קואקסיאלי פרט לאופן TEM יכולים להתקדם אופנים מסדר גבוהה מסוג Transverse Electric

, עבורם הרכיב של השדה החשמלי מתאפס בכיוון התקדמות הגל ואופנים מסדר גבוהה Transverse Magnetic

, עבורם הרכיב של השדה המגנטי מתאפס בכיוון התקדמות הגל. חשוב להיות מודעים לגבי תדר הקטעון (cutoff frequency) הנמוך ביותר עבור האופנים מסדר גבוהה. אם נעבוד מעל תדר קטעון הנ”ל, בקו תמסורת יתקדמו אופנים TEM ואופנים מסדר גבוהה (בעלי מקדמי התפשטות שונים), מה שעלול לגרום לתופעות לא רצויות. עבור קו תמסורת קואקסיאלי, האופן TE11, זהו האופן מסדר גבוהה הדומיננטי (בעל תדר קטעון הנמוך ביותר מבין האופנים מסדר גבוהה). ניתן לחשב את תדר קטעון הנ”ל, מתוך משוואת הגלים 2D

וע”י שימוש בתנאי שפה ניתן לקבל משוואה אופיינית

כאשר:

– רכיב ה – z של השדה המגנטי עבור חתך של קו תמסורת

– מספר גל קטעון (cutoff wavenumber)

– נגזרת של פונקציית Bessel מסוג ראשון, מסדר n

– נגזרת של פונקציית Bessel מסוג שני, מסדר n

את המשוואה הנ”ל לא ניתן לפתור בצורה אנליטית, אלא נדרש לפתור בצורה נומרית. לצורך כך, השתמשנו בפתרון גרפי של המשוואה (איור 8).

נקודת החיתוך הראשונה עם הציר האופקי (פתרון הראשון של המשוואה), התקבלה עבור n=1, לכן מדובר על האופן TE11. קיבלנו . מכאן ניתן לחשב את תדר הקטעון עבור האופן הנ”ל לפי הנוסחא:

בנוסף חישבנו ע”י תוכנת HFSS את התדר הקטעון של הכבל הקואקסיאלי. איור 9 מתאר את הגרף של מקדם התפשטות עבור האופנים TEM ו-TE11.

בסימולציה ע”י שימוש בתוכנת HFSS, קיבלנו תוצאה של תדר הקטעון

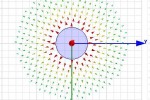
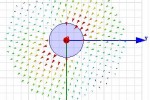
34.54GHz, מה שמאוד קרוב לחישוב האנליטי. כמו כן, ניתן לראות מהגרף האדום, שעבור האופן TEM אין תדר קטעון, כפי שאנו מצפים. בצורה מעשית, מומלץ לקחת מרווח בטחון לפחות של 5%, לכן התדר המקסימאלי שכדאי לעבוד בו בכבל הנתון הינו 32.8GHz. באיורים 10 ו-11 ניתן לראות את הפילוג השדה החשמלי בחתך הכבל עבור האופנים TEM ו-TE11, בהתאמה. פילוג השדה החשמלי עבור האופן TEM הינו רדיאלי.

השיטה שהשתמשנו כאן לניתוח של קו תמסורת קואקסיאלי, מתאימה לסוגים אחרים של קווי תמסורת.