תקשורת אלחוטית באמצעות גלים מילימטריים

תחום ה”גלים המילימטריים” צובר התעניינות רבה בשנים האחרונות, במיוחד על רקע מאמצי התקינה לדור התקשורת הסלולארית הבא, הדור החמישי – 5G, ויישום חלק מרובדי התקשורת בתחום תדרים אלה. בבואנו לתקנן את תקן התקשורת החדש, שיבוסס על גלים מילימטריים, נדרש להבין תחילה את אופי התפשטות האות על פי סוג התווך והאתגרים ביישום תחום לצרכים השונים.

תחום הגלים המילימטריים מוגדר כתחום תדרים החל מ- 30GHz ועד 300GHz. היתרון המרכזי בשימוש בתחום זה נובע מהספקטרום הפנוי ורוחב הסרט הגבוה. , דבר תכונות אלו יכולות לפתור את בעיית ריבוי המשתמשים ההולכת וגדלה בשנים האחרונות, ואשר מהווה את הנטל המרכזי בתכנון הדור הבא של התקשורת הסלולארית. בנוסף, לגלים מילימטריים יתרונות נוספים, כגון ציוד קטן (עקב אורכי גל קצרים) ופוטנציאל מחזור התדר (Frequency re-use) עקב הכיווניות הגדולה של האנטנות והניחות האטמוספרי. אולם יישום הגלים המילימטריים דורש התמודדות עם אתגרים, כגון השפעה מפיזור ובליעה של חלקיקים, ניחות אטמוספרי וכן החזרים ממשטחים וממכשולים.

במאמר הנוכחי מתוארים האתגרים ביישום הנובעים מהשפעת התווך ומתופעת החזרים, כמו כן יוצג מודל התפשטות והשוואת תוצאותיו לניסוי מודל תעלה מוקטן.

אתגרי התפשטות בתווך אטמוספרי
גל אשר מתפשט בתווך האטמוספרי מושפע מהתווך והרכבו: הרכב האוויר היבש, לחות ומשקעים[1]. עקב אורכי הגל הקצרים, בתחום הגלים המילימטריים, מופיעות תופעות של בליעה ופיזור באוויר, המחמירים עם הופעת משקעים, אובך, ערפל ועלייה בלחות (ראה איור 1).

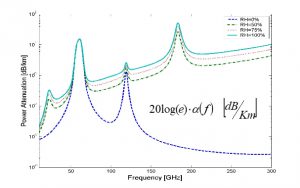
איור 1: ניחות אטמוספרי כתלות בתדר

איור 1 מציג את הבליעה כתלות בתדר בערכי לחות יחסית שונים (RH %), ומראה כי בתדרים מסוימים יש שיאים בניחות הנובעים מבליעה רוטציונית במולקולת החמצן והמים. בנוסף קיימת בליעה מלחות ובמתאר של תקשורת בתנאי ערפל וגשם.

נושא זה נחקר בצורה תאורטית וניסיונית במעבדתנו.

אתגרי תקשורת גמ”מ במבנה סגור

בנוסף להשפעת התווך, ערוץ תקשורת המבוסס על גלים מילימטריים סובל מריבוי החזרים למקלט, העלול לגרום להתאבכויות הורסות ובונות בגלאי, ולקבלת דעיכות בעוצמת הקליטה. בחלל פנימי כמסדרון או חדר, תופעות אלו מתגברות, עקב ריבוי המשטחים המחזירים את האותות. על כן, חשוב לחקור תופעה זו באופן אנליטי ולבחון את השפעותיה על ביצועי הערוץ האלחוטי בתווך פנימי.

עקב אורכי הגל הקצרים של הגלים המילימטריים ניתן לתאר את התנהגותם באופן “קוואזי אופטי” המאפשר להשתמש בכלים מעולם האופטיקה כגון משוואות ההחזרה של פרנל[2]. משוואות פרנל מתארות לנו את עוצמת השדה המוחזר מפני משטח לאחר פגיעת הגל באותו המשטח. מקדם פרנל זה מושפע מקיטוב השידור, וכן מהמקדם הדיאלקטרי של החומר ממנו עשוי המשטח.

על מנת לבחון את מידת ההשפעה של חומרים שונים על התנהגות מודל ההתפשטות, בוצעה סימולציה של מקרה פשוט, בעל החזר בודד מן משטחים בעלי מקדם דיאלקטרי שונה. מקדמי פרנל חושבו בהתאם, ונבחן היחס בין החומרים השונים. איור 2  מציג את מקדמי פרנל כתלות בזווית הפגיעה עבור משטחים מחומרים שונים: אספלט, בטון ועץ-פורמייקה. ניתן לראות כי ערכי מקדמי פרנל משתנים בצורה מועטה בין החומרים, כך שניתן להסיק כי המודל אינו רגיש לשינויים בחומרים המחזירים השונים.

איור 2: ערכי מקדמי פרנל כתלות במקדמים דיאלקטריים שונים

בשימוש במשוואות פרנל נדרש תחילה לאפיין את ההחזרה מפני המשטח, האם היא היא ספקולרית או דיפוזיבית. על מנת להתייחס למשטח כאל משטח ספקולרי, המקיים את משוואות פרנל, קריטריון ריילי צריך להתקיים. בקריטריון זה, חספוס פני המשטח צריך להיות קטן מאורך הגל על פי הנוסחה:

כאשר λ הוא אורך הגל,  -עומק החספוס במשטח ו- – זווית הפגיעה (בין הקרן הפוגעת לבין משטח הפגיעה).

הפעלת הקריטריון עבור אות בתדר של 30GHz, הפוגע בזווית פגיעה של 10° מראה כי ניתן עבור חספוס של 0.72 ס”מ עדיין להתייחס אל המשטח כאל משטח ספקולרי. עקב הכיווניות הגדולה של אנטנות בגלים מילימטריים ניתן לומר שזוויות גדולות יותר מ- 10° כמעט ולא יהיו קיימות ועל כן החספוס שהמשטח יוכל לספוג יגדל, כך שניתן להניח כי המשטחים המחזירים של האות הם בעלי אופי ספקולרי.

מודל קרניים –

“מודל הקרניים” (Ray Tracing model) מתייחס לחזית הגל המתקדמת במרחב כקרן, תוך התחשבות בהפסדי הנתיב כפי שמתוארים במשוואת Friis ובריבוי החזרים[3]. מודל זה הוא פשוט ליישום נומרי, ולוקח בחשבון את קיטוב השידור, את ההחזר מכל משטח (באמצעות מקדמי פרנל) וכן את שבח האנטנה והכיווניות שלה. המשוואה המתארת את מודל הקרניים עבור המקרה הסימטרי בו המשדר והמקלט נמצאים שניהם במרכז[4].

כאשר   הוא הממוצע הגיאומטרי של ההגבר הזוויתי של המשדר והמקלט,  -מקדם הפרנל של כל קרן מוחזרת,  -קבוע הגל הנושא,  -המרחק של הקרן הישירה ו-  -המרחק שכל קרן מוחזרת עוברת.

במשוואה זו הביטוי הראשון מיצג את הקרן הישירה (Line of site-LOS) ושני הביטויים האחרים מייצגים את ההחזרות מהדפנות האנכיות והאופקיות. המשוואה מתחשבת  בקיטובי השידור והשפעתם על אופי ההחזרים מהמשטחים השונים, כמפורט בטבלה 1.

קיטוב האנטנה	החזר מהקירות	החזר מהתקרה והרצפה
אנכי	TE	TM
אופקי	TM	TE

טבלה 1: סוגי ההחזרים בכל משטח כתלות בקיטוב האנטנה

איור 3 מתאר באופן סכמתי את ההחזרים מהקירות, התקרה והרצפה במבנה סגור מאורך, במקרה כללי א-סימטרי.

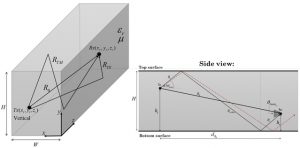
איור 3: מבט על הקרניים המוחזרות בתוך מבנה מאורך

המרחק שכל קרן עוברת תלוי במספר הפעמים בהן היא מוחזרת מהמשטחים. ניתן לחשב אותה באמצעות שיטת השיקופים  (Method of images), המבוססת על חוק סנל. הביטויים הבאים מציגים את אורכם של נתיבי ההתפשטות השונים, עבור תרחיש סימטרי:

הישיר:

וההחזרים:

בנוסף מתחשבים בהשפעת עקום הקרינה של האנטנה המחושבת באמצעות השבח הזוויתי .

השוואה עם ניסויים במודל מוקטן

לצורך אימות המודל בוצעו ניסויי מעבדה ראשוניים במודל מוקטן. נבנה מבנה מאורך  מעץ המצופה פורמייקה (בעל מקדם דיאלקטרי השווה ל-4) בעל ממדים של 10 ס”מ על 20 ס”מ ובאורך של כ-6 מטרים. משדר בתדר 94GHz חובר לאנטנת שופר פירמידית וכן אנטנה זהה נוספת חוברה אל המקלט. ההספק הנקלט בגלאי נמדד כל 1-2 ס”מ, מתחילת אזור השדה הרחוק. השוואה בין תוצאות הסימולציה לניסוי מוצגות באיור 4. האיור מציג את ניחותי הערוץ המתרחשים בתוך המבנה (יחס האות הנקלט לאות המשודר, ב-dB) כתלות במרחק מקלט-משדר.

איור 4: השוואה בין תוצאות הניסוי לסימולציה. קיטוב אופקי (ימין) ואנכי (שמאל)

ניתן לראות התאמה טובה במרבית תחומי המרחק, במגמות עוצמת הקליטה שחושבו במודל האנליטי הפשוט המתבסס על חיבור קרניים ובין אלה שנמדדו. התאמה זו מדגימה כי ניתן לבצע הערכות למאזן תקשורת בערוץ הפועל בגלים מילימטרים גם באמצעות מודל שהוא קוואזי אופטי ומבוסס על ניתוב קרניים כמייצגות את הנתיבים בהם צפוי אות השידור לעבור עד הגיעו למקלט.

סיכום

למחקר זה חשיבות רבה בתחום תקינת ה-5G והבנת התנהגות הגלים המילימטריים בתווכים שונים. ניתוח אנליטי של הבעיות המתרחשות בערוץ תקשורת גמ”מ מסייע לתכנון נכון של ערוץ התקשורת, לחלוקת תאי התקשורת ובחירת מיקומי האנטנות ויכול לחסוך משאבים רבים. בנוסף, הבנה של הבעיות הניצבות בפני ערוץ תקשורת גמ”מ מאפשרת מתן פתרונות מתאימים כגון בחירת תדר עבודה אופטימלי וכן סוגי אנטנות ובכך למטב את יעילות התקשורת בערוץ.

על המחברת:

ליאת רפפורט בעלת תואר שני וראשון בהנדסת חשמל ואלקטרוניקה מאוניברסיטת אריאל. כיום היא דוקטורנטית בהדרכתם של פרופ’ יוסי פנחסי וד”ר גד פנחסי מאוניברסיטת אריאל. עבודת המחקר של ליאת עוסקת בחקירה של ערוצי תקשורת ומכ”מ אלחוטיים בתחומים הגבוהים של הספקטרום האלקטרומגנטי, בתחומי הגלים המילימטריים והתת-מילימטרים ליאת חוקרת במעבדת הגלים מילימטריים והטרה הרץ של פרופ’ פנחסי באוניברסיטת אריאל.