מאמר זה מציג מימוש של מוד תנועה CNC בבקר סרוו, המשלב מבחר של אלגוריתמים מיוחדים לשיפור ביצועי התנועה של המערכת בצירוף דוגמאות ממכונה לחיתוך לייזר.
המימוש מציג שילוב של אלגוריתמי התנועה עם אלגוריתמי הבקרה (עד רמת חוג הזרם של הציר הבודד) כדי להבטיח ביצועי מערכת אופטימליים.
מימוש כזה מתאפשר בטופולוגית בקרה מסוג Central-i שהינה טכנולוגיית בקרה מבוזרת מבחינת ההספק למנועים אך מרכזית מבחינת כול חישובי הבקרה (מסלולי תנועה ובקרת מיקום/מהירות/זרם).
מערכת הבקרה מסופקת עם תוכנת ממשק המאפשרת הפעלה של כול תכונות חישוב המסלול והבקרה בלחיצת עכבר ובדיקת הביצועים באופן מידי.
תנועות CNC:
תנועות CNC הינן תנועות רב ציריות, מסונכרנות עד רמת זמן הדגימה של הבקרה, המורכבות מרצף של (בעיקר) תנועות לינאריות ומעגליות, היוצרות תנועה מרחבית של המכונה/רובוט. זאת להבדיל מתנועות פשוטות, בדידות ולינאריות של ציר בודד (Point To Point) או כמה צירים (תנועת ווקטור).
תנועות CNC מציגות אתגרים רבים, ביניהם:
- עומס חישובי על בקר התנועה (בעיקר כאשר בקר התנועה הינו גם בקר הסרוו של המערכת).
- הורדת נתוני התנועה לבקר בזמן אמת.
- התמודדות עם תנועה בפינות (נקודת המפגש ברף של שתי תנועות לינאריות במרחב).
- כיול המערכת ובחינת ביצועים תוך כדי התנועה המרחבית.
בפרקים הבאים נדגים התמודדות עם קשיים אלו.
המשימה שתשמש כדוגמא במאמר זה:
מכונה לחיתוך לייזר בעלת שני צירים X/Y הנדרשת לבצע חיתוך של מרובע, במהירות גבוהה (עד 0.5 מטר לשנייה), עם פינות ברדיוס של 2 מ”מ, תוך כדי שמירה על המגבלות הבאות:
- המהירות לכול אורך התנועה, כולל בפינות, לא תחרוג מ- ±3% מהמהירות הנומינאלית.
- שגיאת מיקום מרחבית, לכול אורך התנועה ובפינות, קטנה מ- 40 מיקרון.
צירי X, Y ממומשים עם מנוע ליניארי ואנקודרים של 0.5 מיקרון.
הורדת עומס חישובי ועומסי תקשורת:
תנועות CNC מוגדרות (בדרך כלל) על ידי קובץ G Code שמגדיר תנועה רציפה לאורך זמן, המורכבת מסדרה של סיגמנטים (כול סיגמנט מגדיר מקטע ליניארי או קשת, בדרך כלל). את הקובץ יש להוריד לבקר תוך כדי התנועה (כדי למנוע מגבלת גודל ולקצר את זמן הביצוע של כול התהליך). על הבקר לעבד את הקובץ בזמן אמת (להפוך אותו לפקודות תנועה בפועל, לחשב פינות וכדומה) ובמקביל לאפשר תקשורת נכנסת בקצב גבוה עם הגדרות של סיגמנטים חדשים.
הבקר המדובר (של חברת אגיטו) מסופק עם ספריה להתמרת G Code לשפה פנימית של הבקר, המבטיחה יעילות (מבחינת נפח זיכרון ומהירות הורדה התקשורת, כמו גם מבחינת עיבוד הנתונים בבקר לקראת התנועה בפועל).
נתונים לדוגמא:
- עומק CNC FIFO של אלפי סיגמנטים.
- קצב הורדה של סיגמנטים חדשים: כ- 50 סיגמנטים בשלוש מילי שניות!
הבקר מסופק עם תוכנה המאפשרת הפעלה פשוטה של תהליכי תנועה מורכבים, אותם ניתן לייבא מ- G Code או לייצר ידנית בפשטות, כפי שניתן לראות בתמונה מספר 1.
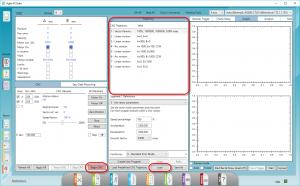
איור 1: ממשק הפעלה בסיסי לתנועות CNC של חברת אגיטו
זמן הורדה של כ- 50 סיגמנטים בשלוש מילי שניות, כולל בתוכו גם חישוב והוספה של פינות אוטומטיות ו/או אלגוריתמי תנועה נוספים להתמודדות עם פינות, כמתואר בהמשך. רוב החישובים המיוחדים מתבצעים עם דחיפת הסיגמנטים ל- CNC FIFO (כולל בדיקה של חוקיות הסיגמנטים) כך שבזמן אמת, בפסיקת התנועה והבקרה, החישובים מצטמצמים למינימום ההכרחי.
התמודדות עם פינות:
קבצי G קוד רבים מתארים את התנועה כרצף של קווים ליניאריים. ברוב המקרים, התנועה מוגדרת כתנועה במהירות אחידה (מהירות וקטורית אחידה, לאורך מסלול התנועה), ללא עצירה בפינות (נקודת המעבר בין קו מרחבי לינארי אחד, לזה שאחריו).
תנועה כזו אינה אפשרית באופן פיזיקלי. לא ניתן לשנות את כיוון התנועה, לשמור על המהירות וקטורית אחידה ולעבור על מסלול התנועה של שני הקווים הליניאריים בו זמנית. תנועה כזו דורשת תאוצה אינסופית מצירי התנועה.
ניסיון לבצע תנועה כזו יבטיח אומנם פקודת מיקום מדויקת, אך הצירים יחוו פקודת תאוצה אינסופית (פקודת מדרגה במהירות) ושגיאות העקיבה של הצירים תהיינה גבוהות (ובדרך כלל תנודתיות).
מערכות CNC מאפשרות שיטות שונות להתמודד עם נקודת המעבר, כאשר על המשתמש לבחור את השיטה המתאימה בהתאם לאפליקציה. מצד אחד ניתן, למשל, “לעגל” את הפינה כמתואר באיור 2, ולהבטיח תנועה חלקה יותר במהירות תנועה וקטורית קבועה, אבל עיגול כזה, שמבטיח תנועה “חלקה” יחסית, מכיל בתוכו שגיאת מסלול (המסלול אינו עובר בנקודה B שהוגדרה כחלק מהמסלול הנדרש). ככול שרדיוס הפינה גדול יותר, תתאפשר תנועה חלקה יותר, אך גם תיווצר שגיאה גדולה יותר (וזאת גם אם שגיאת המיקום של הצירים תהיה אפס… השגיאה היא ברמת מסלול התנועה).
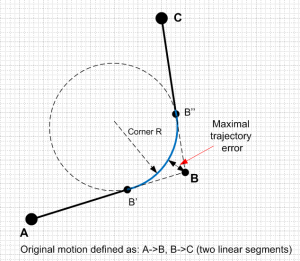
איור 2: פינה “מעוגלת” ושגיאת המיקום הנוצרת במסלול התנועה עצמו
בעיה נוספת שמתעוררת בתנועה בפינות הינה שבאופן מפתיע, למרות שלמראית עין מסלול התנועה הינו חלק ורציף לגמרי, הרציפות מתקיימת רק בפקודות המיקום והמהירות של כול אחד מהצירים המשתתפים בפינה, בעוד שכול אחד מהצירים חווה קפיצה משמעותית באפס זמן בפקודת התאוצה (אחד מהצירים בכניסה לפינה והשני ביציאה ממנה). כול ציר “סובל” ממכת Jerk אינסופית בכניסה (או ביציאה) מהפינה, ולכן ביצועי התנועה בפינה אינם מושלמים ובדרך כלל (תלוי במהירות התנועה) מתעוררת שגיאת מיקום גדולה הפוגמת באיכות התנועה המרחבית (צורת הפינה).
איור מציג 3 מציג את פקודות המיקום, מהירות ותאוצה של אחד הצירים, בפינה של 90 מעלות (כול המשתנים מנורמלים כדי להיכנס למערכת צירים אחת). החץ מצביע על קפיצת התאוצה בכניסה לפינה.
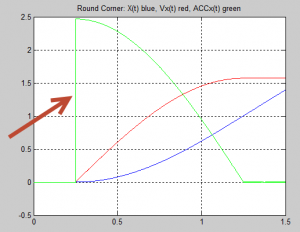
איור 3: התנהגות פקודות המיקום (כחול), מהירות (אדום) ותאוצה (ירוק) של אחד הצירים בפינה של 90 מעלות
בקרים שונים מאפשרים אלגוריתמים שונים כדי לאפשר תנועה חלקה ככול האפשר בפינות, תוך כדי הקטנת השגיאה שנוצרת (הן שגיאה המסלול עצמו והן שגיאת העקיבה של הצירים), כמו גם אופציות לחישוב אוטומטי של פינות מסוגים שונים, כאשר לכול סוג פינה יש את היתרונות והחסרות המובנים שלו (כאמור למעלה, לפינה הבנויה בצורת קשת של מעגל יש חיסרון של Jerk אינסופי לכול אחד מהצירים המשתתפים).
הבקר שבו נעשה שימוש במכונה המדוברת (בקר של חברת אגיטו) כולל את התכונות הבאות לאופטימיזציה של התנועה (ברמת מסלול CNC המרחבי וברמת הצירים הבודדים המשתתפים בתנועה):
- אפשרות לקביעת פרמטרים הפינות (סוג, רדיוס, שגיאה מרבית…) כפרמטרי גלובליים או לכול קבוצת פינות בנפרד.
- הוספה אוטומטית של פינות על פי קריטריונים הנקבעים על ידי המשתמש.
- תמיכה בסוגי פינות שונים.
- הגדרת מגבלת תאוצה לכול ציר ובהתאמה שינוי המהירות בפינה כדי לא לחרוג מהמגבלות של הצירים.
- הגדרת פינה על פי רדיוס או על פי שגיאת מסלול מרבית.
- אפשרות לפינה מעוגלת, או פינה ללא קפיצה בתאוצה, או תנועה ללא יצירת פינה, אבל עם מגבלה בקפיצת המהירות לכול ציר (לאפליקציות בהן הכרחי לעבור דרך נקודה B באיור מספר 2, אך ללא לבצע עצירה ממש בנקודה B).
איורים 4 ו- 5 מציגים דוגמאות לקביעה (חלקית) של פרמטרי התנועה בפינה.
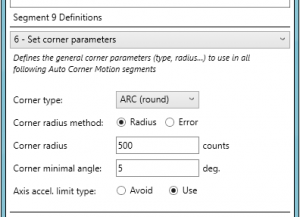
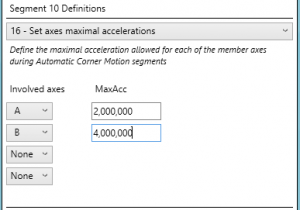
איורים 4 ו- 5: קביעת פרמטרי תנועה בפינה בבקר התנועה
סוגי מסלולי הפינה השונים, כמו גם האלגוריתמים השונים לקביעת המהירות בפינה, מאפשרים למשתמש להתאים את התנועה באופן האופטימאלי לאפליקציה הנדרשת.
במקרה של הדוגמא המדוברת, נעשה שימוש בפינות מעוגלות על פי דרישות הלקוח, ברדיוס נקוב של 2 מ”מ (שוב, על פי דרישות הלקוח) ובתנועה במהירות קבועה לכול אורך המסלול שנדרשת כדי לשמור על איכות החיתוך של הלייזר. אי לכך, מרב המאמץ הופנה לאלגוריתמי הבקרה כדי להבטיח תנועה אופטימאלית בפינות. על כך בפרק הבא.
אופטימיזציה של ביצועי תנועה בפינות:
כדי להציג את הבעיה שעמדה בפנינו, מוטב להציג את ביצועי התנועה כפי שהיו לאחר כיול מטבי של כול אחד מצירי התנועה בפני עצמו, אך ללא אלגוריתמי בקרה מיוחדים לתנועת ה- CNC. איור מספר 6 מציג צילום של חיתוך הלייזר במצב זה. ניתן לראות, גם ללא הגדלה, את התנודה לאחר הפינה (חץ אדום). גם הפינה עצמה אינה מעוגלת כנדרש. איור 7 מציג הקלטה של שגיאות המיקום במשך התנועה, כאשר נקודות הכניסה לפינות מסומנות בחיצים. משך התנועה בפינה הינו רק כ- 12 מילי שניות, אך ההשפעה של ה- Jerk האינסופי נמשכת זמן רב גם אחרי היציאה מהפינה!
יש לציין שקפיצת התאוצה הינה בגובה של כ- 2.5 ג’י (באפס זמן) והזרמים הרגעיים למנוע מגיעים עד ל- 50 אמפר. אכן פינה “אגרסיבית”…

איור 6: ביצוע חיתוך לייזר בפינה (ואחרי הפינה) לפני הפעלת האלגוריתמים המיוחדים
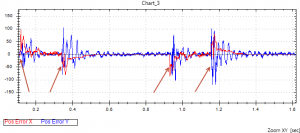
איור 7: ביצוע תנועה בפינה (ואחרי הפינה) לפני הפעלת האלגוריתמים המיוחדים
ולפני שניגש לתיאור האלגוריתמים השונים, איורים 8 ו- 9 מציגים את ביצועי התנועה בסיום התהליך, עם שימוש בכול האלגוריתמים המתוארים להלן. הפעם התמונה של ביצועי חיתוך הפינה סופיים מובאת בהגדלה של x50 ! וגרף שגיאות העקיבה של הצירים מובא באותו Scaling כמו הגרף המוצג באיור 7. ניתן לראות שהתנודות נעלמו ושהרדיוס האמצעי נמצא עמוק בתוך דרישת הדיוק (המספרים נתונים במילימטרים), כאשר הביצועים היו דומים בכול ארבעת הפינות (אין הדבר פשוט, מכיוון שבכול פינה הביצועים הנדרשים מכול ציר שונים) וכמובן, בהתאמה, שגיאות המיקום קטנות בערך פי 5!
יש לציין שכמובן, מהירות התנועה הווקטורית הייתה זהה לאורך כול הניסוי. השיפור הושג על ידי אלגוריתמי התנועה והבקרה המיוחדים, ולא על ידי האטת התנועה בפינות (בלתי אפשרי על פי דרישות האפליקציה).
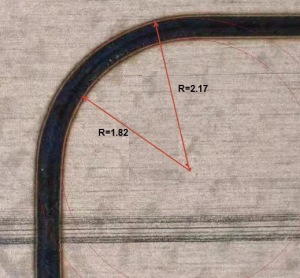
איור 8: ביצוע חיתוך לייזר בפינה (ואחרי הפינה) אחרי הפעלת האלגוריתמים המיוחדים
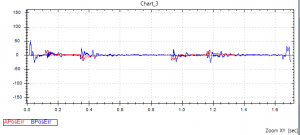
איור 9: ביצוע תנועה בפינה (ואחרי הפינה) אחרי הפעלת האלגוריתמים המיוחדים
אם כך, כיצד הוצג השיפור הבולט בביצועי התנועה?
הבקר שבו נעשה שימוש מציע את התכונות הבאות:
- Anti-Friction within (between) CNC segments. כדי לאפשר התחלת תנועה מהירה לציר שהיה בעמידה לפני תחילת כול סיגמנט תנועה.
- הפעלת פילטרים מיוחדים, על המיקום ועל המהירות, כדי להחליק את השפעת ה- Jerk האינסופי, כמעט מבלי לפגוע במסלול המרחבי של הפינה וכמעט מבלי להשפיע על המהירות הווקטורית (כול השינויים הינם עמוק בתחום המותר על ידי האפליקציה).
- CNC Gain Scheduling: יכול לשנות את פרמטרי הבקרה של כול אחד מהצירים בעת שהתנועה חולפת דרך הפינה ולמשך זמן מסוים לאחר הפינה, כמתואר באיור מספר 10.
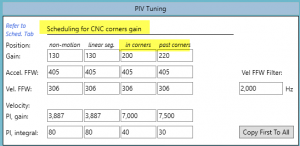
איור 10: פרמטרי בקרה במוד CNC Gain Scheduling
תכונות משלימות לאפליקציה מסונכרנת:
בעוד שתנועת CNC מגדירה את מסלול התנועה והתזמון של התנועה עצמה, אפליקציה שלמה אינה כוללת רק תנועות אלא גם הפעלות שונות. במדפסת תלת ממד נדרש למשל לשלוט על גוף החימום של חומר ההדפסה (ולעיתים להמתין עד להצבתו בטמפרטורה מסוימת) וגם לשלוט על צירים נוספים שאינם חלק מתנועת ה- CNC אך צריכים להיות מסונכרנים להתקדמות שלה. במכונה לחיתוך לייזר נדרש להפעיל ולכבות את הלייזר ולעיתים גם לשלוש בעוצמה שלו.
הבקר בו נעשה שימוש מאפשר לשלב, בין סיגמנטי התנועה, גם סיגמנטים ניהוליים המאפשרים שליטה על יציאות, המתנה לכניסות, השמה למשתני בקר והמתנה למשתני בקר, וזאת מבלי להשפיע על התנועה עצמה, אך באופן מסונכרן אליה לחלוטין. באמצעות סיגמנטים מסוג זה, בשילוב תוכנת משתמש, ניתן לייצר בקלות אפליקציה שלמה ומסונכרנת עם מסלול התנועה של ה CNC. איור מספר 11 מציג דוגמא של סיגמנט מיוחד כזה: השמה למשתני בקר והמתנה למשתנה אחר שיקיים תנאי כלשהו לפני המשך של תנועת ה- CNC. ניתן גם להפעיל יציאות דיסקרטיות תוך כדי תנועה ובין סיגמנטים, באופן מסונכרן.
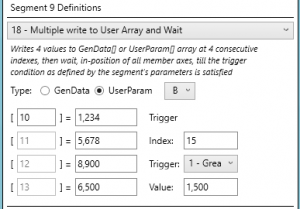
איור 11: סיגמנט השמה והמתנה לאירוע בבקר, לסנכרון התנועה עם אירועים חיצוניים והחלטות פנימיות בבקר
לסיכום:
מאמר זה מציג את הקשיים להשגת ביצועים גבוהים בתנועות CNC ואת השיטות השונות בהן נעשה שימוש באמצעות הבקר של חברת אגיטו כדי להגיע לביצועים הנדרשים, כפי שהודגמו באמצעות אפליקציית חיתוך לייזר בעלת דרישות אגרסיביות.
על הכותב:
אייל ספיר הינו מייסד ובעלים משותף של חברת אגיטו מערכות הינע. אייל הינו בעל ניסיון רב שנים בתחום בקרת התנועה, בארץ ובעולם ועוסק בפיתוח ושיווק מוצרי מערכות בקרה (אלגוריתמים, תוכנה וחומרה
















