שיטות למציאת כוון הגעה של גלים אלקטרומגנטיים-סקירה מדעית

מציאת כוון הגעה של אותות אלקטרומגנטיים (קורנים או החזרים) המשודרים במרחב הינו צורך הכרחי, חיוני ובעל חשיבות עליונה הן לצרכים צבאיים ביטחוניים והן לצרכים אזרחיים הקשורים בחיי אדם.

ניתוח אותות אלו ע”י מערכות “חכמות” הפועלות כמעט באפס זמן מהווה נדבך חשוב והכרחי למתן מענה מיידי והולם בהתאם לסוג המטרה ותכונותיה. (מטרה נחה, מטרה נעה במהירות נמוכה, במהירות בינונית או במהירות גבוהה)

מרחב ההתמודדויות עשוי להוות זירה צפופה ומורכבת, כך שייתכן ולא יהיה ניתן לטפל בכל התרחישים באמצעות מערכת אחת בלבד, אלא באמצעות מספר מערכות משולבות.

מרחב זה, ככל שנלמד אותו היטב, יאפשר את השילוב האופטימלי של המערכות הנדרשות למתן מענה מיטבי בזירת המטרות והקורנים.

להלן סיווג פשטני של המערכות הנדרשות כפונקציה של סוגי המטרות והקורנים;

• מערכות נייחות מול מטרות או קורנים נייחים
• מערכות נייחות מול מטרות או קורנים נעים
• מטרות נעות מול מטרות או קורנים נחים
• מטרות נעות מול מטרות או קורנים נעים

כמובן שהמערכות (בעיקר הצבאיות) תהיינה משולבות בפלטפורמות קרקעיות, ימיות ואף אוויריות. המורכבות של כל מערכת תהיה בהתאם  לתנאי הסביבה של כל פלטפורמה וחלקן אף יתממשקו למרכיבים מכאניים וחשמליים של הפלטפורמה. (נתוני ניווט, מהירות ועוד)

בתחום הצבאי

גילוי מטרות על בסיס הד חוזר (Echo) – מערכות מכ”ם

גילוי כוון אותות מכ”ם (קורנים) המשודרים ממטרות במרחב  – מערכות לוחמה אלקטרונית

• מערכות פאסיביות – Electronic Support Measures (ESM)
• מערכות אקטיביות – Electronic Counter Measures (ECM)

גילוי כוון אותות תקשורת  – Communication Intelligence (COMINT)

• מערכות Direction Finding (DF) בתחום ה-HF
• מערכות Direction Finding (DF) בתחום ה-VHF
• מערכות Direction Finding (DF) בתחום ה-UHF

בתחום האזרחי

איתור אנשים מ-תחת להריסות

איתור אנשים מ-תחת למפולות שלגים

איתור אנשים “אבודים” ביערות או בג’ונגלים

הפיתוחים המתקדמים ביותר במערכות לשימוש זה נעשו בעיקר בתחום הצבאי, כאשר המרכיב החישובי אומץ במערכות אזרחיות תוך ויתור מראש על כושר הרזולוציה ומרחקי הדיוק המרחבי דו מימד ותלת מימד.

בסריקה היסטורית על פני 30 השנים האחרונות אנו מוצאים את השיטות הבאות:

• שיטת השוואת אמפליטודה Amplitude Comparison
• שיטה אינטרפרומטרית Interferometric
• שיטה לחישוב זמני הגעה Time Of Arrival (TOA)
• שיטה לחישוב הפרש זמני הגעה Time Difference Of Arrival
• שיטה לחישוב הפרשי פאזות

בחלק הבא נפרט כל שיטה בנפרד ונסכם בטבלת השוואה את היתרונות וחסרונות של כל שיטה ושיטה.

 

השוואת אמפליטודה Amplitude Comparison

במערכות מכ”ם, החל משנות ה-70 השתמשו בשידור אלומה סורקת באופן מאוד מוגבל יחסית תוך שימוש בטכניקת Conical Scan, כלומר סריקה קונית גזרתית. הסריקה בוצעה ע”י

• שיטה מכאנית – האנטנה עצמה ביצעה סריקה סיבובית מכאנית באופן קוני כך שתוך כדי סיבוב האנטנה, האלומה שודרה לכוון אחר.
• שיטה אלקטרונית – הסריקה בוצעה באופן אלקטרוני על בסיס שינויי פאזה

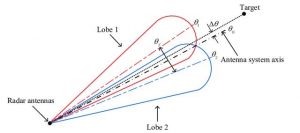
באיור 1 למטה, רואים את 2 האלומות ב-2 זמנים שונים כך שהפרש הזווית θ בין מרכזי האלומה מתאר את הזווית הקונית של סיבוב האלומה.

 

איור 1 – תיאור 2 אלומות במרחב בזמנים שונים

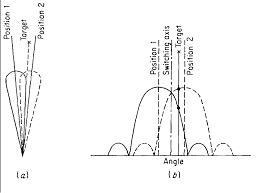
באיור 2 למטה, רואים את תיאור האלומות במישור התדר (כולל אונות צד)

 

איור 2 – תיאור 2 האלומות במישור התדר

עקרון הפעולה בשיטה זו מבוסס על מדידת ההספק החוזר ממטרה בכל רגע נתון בו ידוע מראש כיוון ההסתכלות של האנטנה, לאחר סיום סבב שלם, בוחרים את התוצאה הגבוהה ביותר והיא מעידה על כוון המטרה.

במערכות מסוג Monopulse, קימות 4 אנטנות במערך כאשר 2 אנטנות בכל תת מערך והמרחק בין 2 אנטנות בכל תת מערך הוא d. משתמשים בחישוב האלומות ב-2 מצבים, סכום האלומות והפרש האלומות ב-2 מצבי אזימוט כפי במוראה באיור 3 למטה.

איור 3 – תיאור האלומות סכום והפרש במערכת Monopulse

שיטת החישוב במקרה זה, מתבססת על הביטוי

כאשר: d הינו המרחק בין 2 אנטנות בל תת מערך ו- אורך הגל של תדר המכ”ם.

שיטה אינטרפרומטרית Interferometric

בשיטה זו מודדים את הפאזה של האות הנקלט בכל אנטנה במערך (המרחק בין האנטנות נקרא Baseline והוא נדרש להיות מספיק גדול יחסית על מנת לאפשר שינויי פאזה בסדרי גודל סבירים)

בחישוב אלגוריתמי של הפרש הפאזות ניתן לקבל בדיוק סביר את כוון או מיקום המטרה.

כמובן שבמקרה ומדובר על מטרה נעה, הרי שהפרש הפאזה יחושב בתאם, על מנת למנוע שגיאות הנובעות מהפרש אנטי-פאזי, המערכת מכילה רכיב קורלטור לתיקון השגיאה.

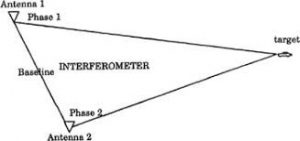
באיור 4 למטה, רואים מקרה פרטי של 2 אנטנות במערך הסנסור. ככל שיהיו יותר אנטנות, הרי שדיוק המדידה יהיה גבוה יותר.

איור 4 – תיאור 2 אנטנות במערך אינטרפרומטרי

באיור 5 למטה, רואים מערך אינטרפרומטרי של 4 אנטנות ספירליות

איור 5 – מכלול 4 אנטנות ספירליות במערך אינטרפרומטרי

שיטה לחישוב זמני הגעה Time Of Arrival (TOA)

בשיטה זו מודדים את זמן ההגעה בכל אחת מאנטנות המערך, מאחר והאנטנות מפוזרות במרחקים שווים (או שונים וידועים מראש) הרי שניתן לדעת את הגודל הסקלרי של תוספת המרחק בכל ציר של אנטנה ביחס למקור הקורן וע”י חישוב גיאומטרי פשוט ניתן לדעת את זווית ההגעה. כמובן שהמרחק שעובר הגל מיוחס למהירות האור. (C=3×10⁸ m/s)

גודל המרחק העודף שעובר הגל שנקלט ע”י אנטנה מס’ 2 ביחס למרחק שעובר הגל הנקלט באנטנה מס’ 1 הינו

אם נחשב את הפאזה של גודל זה הרי שנקבל   ואז ניתן לחשב את הזווית מתוך הביטוי:

נבצע חישוב זה ע”י הפרש הפאזה בין כל אנטנה במערך לבין אנטנה מס’ 1 וע”י כך נוכל לקבל תוצאה מדויקת של זווית ההגעה θ.

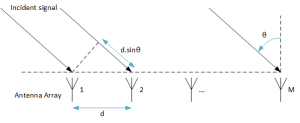
באיור 6 למטה רואים מערך של M אנטנות כאשר זווית הגל הפוגע הינה θ.

איור 6 – מערך תיאורטי של M אנטנות לחישוב זמני הגעה TOA

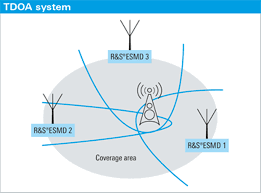
שיטה לחישוב הפרש זמני הגעה Time Difference Of Arrival (TDOA)

בשיטה זו, מותקן סנסור קליטה בכל קודקוד של משולש המערך (אורך בסיס ארוך או קצר, בתלות בגודל הפלטפורמה או בדיוקי מדידה)

בכל סנסור מחושב כוון הגעת הגל המתקבל ע”י אליפסה, כל שלמעשה מתקבלות במקרה שלנו 3 אליפסות כך שהתוצאה הסופית הינה שטח החתך של 3 האליפסות, כפי שמוראה באיור 7 למטה.

איור 7 – מערך תיאורטי של 3 סנסורים לחישוב הפרשי זמני הגעה TDOA

להלן טבלת סיכום המשווה את הפרמטרים בכל שיטה ושיטה.

רמת שגיאות	רוחבי אלומה	מרחק יחסי של המטרה	מרחק בין אנטנות	מס’ אנטנות	פרמטר-שיטה
גבוהה	צרה	בינוני ארוך	גדול	2-3	Amplitude Comparison
בינונית	צרה	בינוני	קצר	4-5	Interferometer
בינונית	רחבה	בינוני – ארוך	ארוך	3-4	TOA
נמוכה	צרה	בינוני – ארוך	קצר	4	TDOA

 

REFERENCES

[1]   Demmel F. “Practical aspects of design and application of Direction Finding Systems,” Elsevier Inc. 2009.

[2]   Gething, P. J. D. “Radio Direction Finding and Super resolution,” Peter Peregrinus Ltd. London 1990.

[3]   Lim, J. S., Chae, G. S. and Park, Y. C., “A Novel Technology of Microwave Direction Finding with a Combination of Amplitude measurement and Phase measurement,”, Proceeding of ISAP 2005, 2005.

[5]   Robert J. Mailloux, “Phased Array Antennas Handbook,” Artech House, 2nd Edition, pp. 1-43, 2005.

[6]   Robert C. Hansen, “Phased Array Antennas,” Wiley, 2nd Edition, pp.186-232, 2010.

[7]   Eli Brookner, “Practical Phased Array Antenna Systems,” Artech House, pp. 85-102, 1991.

[8]   Tuncer T. E. and Friedlander, B. (Ed) “Classical and Modern Direction of Arrival Estimation,” Elsevier Inc. 2009.

[9]   E. Grosicki and K. Abed-Meraim, “A New Trilateration Method to Mitigate the Impact of Some Non-Line-of-Sight Errors in TOA Measurements for Mobile Localization,” Proc. Int’l Conf. Acoustics, Speech, and Signal Processing, vol. 4, pp. 1045-1048, Mar. 2005.

[14] Y. T. Chan and K. C. Ho, “Simple and efficient estimator for hyperbolic location,” IEEE Transactions on Signal Processing, vol. 42, no. 8, pp. 1905-1915, 1994.