1.אימפדנס של אנטנות
אנטנות קטנות ניתנות לתיאור סכמטי על ידי מעגל RLC אלמנטרי הכולל נגד עם התנגדות ממשית R, קבל עם קיבול C וסליל עם השראות L. אנטנות תיל ישרות כגון דיפול ומונופול מתנהגות בדומה למעגל טורי ואילו אנטנות תיל מסוג לולאה כגון לולאה עגולה, לולאה ריבועית או סליל מתנהגות בדומה למעגל מקבילי. נגביל את הדיון הנוכחי למעגל תהודה טורי בלבד. ההרחבה למעגל מקבילי היא פשוטה על ידי שימוש באדמיטנסים במקום בראקטנסים.
נתבונן באיור 1 [1] המציג אנטנה כמעגל RLC טורי הכולל 4 רכיבים:
- התנגדות ממשית המיוחסת להפסדים פנימיים באננה RL
- התנגדות ממשית המיוחסת למנגנון הקרינה (התנגדות קרינה) Rr
- ריאקטנס מדומה הכולל סליל וקבל XA= jωL + 1/jωC
ω הוא התדר המעגלי ו-f היא התדירות ביחידות Hz
האנטנה מחוברת לקו תמסורת עם אימפדנס אופייני Zo
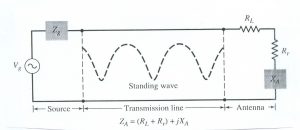
איור 1 :מעגל תמורה סכמטי של אנטנה קטנה המחוברת לקו תמסורת. קרדיט [1]
אימפדנס הכניסה המרוכב של האנטנה יהיה אפוא
- ZL (ω) = R(ω) + jXA(ω) = R(ω) + jωL + 1/jωC
כאשר התדר נמוך מאד, אימפדנס הכניסה שואף ל-∞. כאשר התדר גבוה מאד, אימפדנס הכניסה שוב שואף ל-∞. בתדר התהודה, המוגד על ידי (2), האימפדנס שואף ל-R.
- ω² = 1/LC
2. מקדם החזרה
כאשר האנטנה מחוברת לקו תמסורת עם אימפדנס אופייני Zoנוצרת החזרה של הגלים המגיעים לאנטנה מן הגנרטור. ביטוי כולל למקדם ההחזרה המרוכב (למתח) G נתון על ידי [2]-[3]:
(3) Γ = (ZL – Zo) / (ZL + Zo)
כאשר ZL הוא העומס, כמתואר במשוואה (1).
החלק הממשי של מקדם ההחזרה מסומן בדרך כלל על ידי r
(4) ρ= |Γ|
מקובל לחשב ולמדוד את מקדם ההחזרה בסקלה לוגריתמית כפונקציה של התדר ומתוך כך להגדיר את רוחב הסרט היעיל של האנטנה לפי תנאי רצוי של מקדם ההחזרה. למשל באיור 2 רואים את מקדם ההחזרה הלוגריתמי ואת רוחב הסרט בנקודות -10 dB
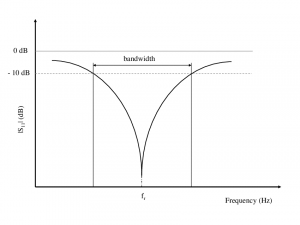
איור 2 גרף של מקדם ההחזרה בתלות בתדר ורוחב הסרט בנקודות -10 dB
3. יחס גלים עומדים
יחס הגלים העומדים לאורך קו התמסורת VSWR מוגדר על ידי [2]-[3]:
(5) VSWR = (1 + ρ) / (1 – ρ)
טבלת המרה שימושית בין מקדם החזרה לבין יחס גלים עומדים מובאת להלן:
Return Loss |Γ| Reflected power VSWR
——————————————————————————————–
-∞ 0 0% 1
-40 dB 0.01 0.01% 1.01
-30 dB 0.0316 0.1% 1.07
-25 dB 0.0562 0.3% 1.12
-20 dB 0.1 1% 1.22
-19 dB 0.1122 1.2% 1.25
-16 dB 0.1585 2.5% 1.38
-14 dB 0.2 4% 1.50
-12 dB 0.2512 6.3% 1.67
-10 dB 0.3162 10% 1.92
-9.5 dB 0.3333 11% 2.00
-8.0 dB 0.398 16% 2.32
-6.0 dB 0.5 25% 3.00
-4.0 dB 0.630 40% 4.40
-3.0 dB 0.707 50% 5.85
-2.0 dB 0.795 63% 8.75
-1.0 dB 0.89 80% 17.2
0 dB 1 100% ¥
ננסה עתה להמיר את מקדם ההחזרה בתלות נתדר ביחס הגלים העומדים בתלות בתדר [4-5].
נסמן את העומס המנורמל על ידי:
(6) Z = r + jx
r = R/Zo
x = X/Zo
ונקבל
(7) ρ = |(1 + jx -1)| / |1 + jx +1) = |x| / √ x² + 4
ועל ידי הצבת (7) לתוך (5) נקבל:
(8) VSWR = [1 + |x|/(√x² + 4)] / [1 – |x|/(√x² + 4)]
ובהמשך:
(9) VSWR = [√x² + 4) + |x| / [√x² + 4) – |x|]= [(√x² + 4) + |x|) / 2|]2
(10) √VSWR = (√x² + 4) + |x|) / 2
(11) √VSWR – 1/√VSWR = (√x² + 4) + |x|) / 2 – (2√x² + 4 – |x|) / 4 ≈ |x|
4. מקדם הטיב Q
לאחר שלבים נוספים (המתוארים בפירוט ב-[5-6]) מגדירים את גורם הטיב של מעגל התהודה Q ומקשרים אותו לרוחב הסרט ה”טבעי”. הגדרת מקדם הטיב היא – סך האנרגיה האגורה במהוד כפול 2p חלקי האנרגיה המתבזבזת במחזור אחד.
- 2π x stored energy / dissipated energy in one cycle
בסליל, האנרגיה האגורה היא 2 LI²/ (L היא ההשראות, I הוא הזרם השיאי) והאנרגיה המתבזבזת היא I²R/2f, לכן גורם הטיב של סליל+נגד הוא
- Q = 2π fL / R = XL / R
בקבל, האנרגיה האגורה היא CV²/2(C הוא הקיבול, V הוא המתח השיאי) והאנרגיה המתבזבזת היא V²/2fR, לכן גורם הטיב של קבל+נגד הוא
(14) Q = 2π f CR = R / XC
במעגל תהודה אפשר להגדיר את Q הן לפי (13) והן לפי (14). רוחב הסרט של מעגל התהודה הוא הפוך לגורם הטיב. נשתמש במונח של רוחב סרט יחסי
(15) Fractional bandwidth = Δf/f = 1/Q
וזה קורה בנקודות בהן ההספק יורד לחצי (נקודות 3 dB) שבהן גם |x| = R.
5. רוחב הסרט לפי יחס גלים עומדים
הקשר בין רוחב הסרט עבור יחס גלים עומדים נתון כלשהו VSWR, לבין רוחב הסרט בנקודות חצי ההספק, נתון על ידי [5]-[6]:
(16) BW(@VSWR) = BW(3dB) (VSWR-1) / 2 √VSWR
נדגים באיור 3 שבו מסומנים רוחבי הסרט (BW = f2 – f1) עבור ערכים שונים של VSWR.
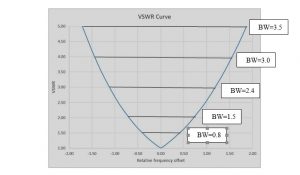
איור 3 התלות של VSWR בתדר עבור מעגל תהודה טורי אידאלי
רוחב הסרט בנקודות 3 dB נתון בגרף על ידי BW (@VSWR=5.85) = 3.8
רוחבי הסרט בנקודות VSWR אחרות נתונים על ידי (16). נשווה את הערכים המתוארים באיור 3 לעומת הערכים המתוארים על ידי הקירוב (16).
לפי איור 3 BW 16 לפי נוסחהBW
———————————————————————————————–
BW(@VSWR=5.7) 3.8 3.8x(VSWR-1)/2√VSWR = 3.8
BW(@VSWR=5.0) 3.5 3.8x(VSWR-1)/2√VSWR = 3.4
BW(@VSWR=4.0) 3.0 3.8x(VSWR-1)/2√VSWR = 2.9
BW(@VSWR=3.0) 2.4 3.8x(VSWR-1)/2√VSWR = 2.2
BW(@VSWR=2.0) 1.5 3.8x(VSWR-1)/2√VSWR = 1.3
BW(@VSWR=1.5) 0.8 3.8x(VSWR-1)/2√VSWR = 0.8
רואים שהקירוב סביר בהחלט.
דוגמה אחרת מוצגת באיור 4. נניח שיצרן מדווח על רוחב סרט יחסי בנקודות VSWR=2 לפי BW=12% ונשאל מהו רוחב הסרט בנקודות VSWR=4 וכן VSWR=5.85
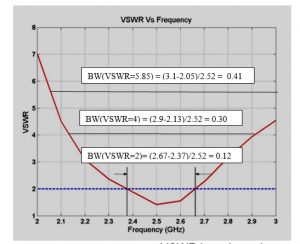
איור 4 התלות של VSWR בתדר עבור אנטנה מעשית
פתרון לפי הגרף, בנקודות VSWR = 4
BW(@VSWR=4) = (2.9-2.13)/2.52 = 0.30
פתרון מקורב לפי משוואה (16):
BW(@VSWR=4)/BW(@VSWR=2) = (4-1)/√4 / (2-1)/√2 = 2.1
BW(@VSWR=4) = 0.12 x 2.1 = 0.25
פתרון לפי הגרף, בנקודות VSWR = 5.85
BW(@VSWR=5.85) = (3.1-2.05)/2.52 = 0.41
פתרון מקורב לפי משוואה (16):
BW(@VSWR=5.85)/BW(@VSWR=2) = (5.85-1)/√5.85 / (2-1)/√2 = 2.8
BW(@VSWR=4) = 0.12 x 2.8 = 0.34
דוגמה נוספת מוצגת באיור 5. נניח שיצרן מדווח על רוחב סרט יחסי בנקודות VSWR=2 לפי BW=3.3% ונשאל מהו רוחב הסרט בנקודות VSWR=3. נזכור כי בנקודות VSWR=2 מקדם ההחזרה הוא RL=-9.5 dB ובנקודות VSWR=3 מקדם ההחזרה הוא RL=-6 dB.
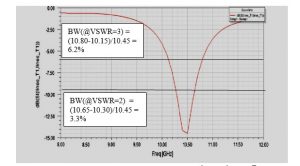
איור 5 התלות של מקדם ההחזרה בתדר עבור אנטנה מעשית
פתרון לפי איור 5:
BW(@VSWR=2) = (10.65-10.30)/10.45 = 3.3%
BW(@VSWR=3) = (10.80-10.15)/10.45 = 6.2%
פתרון מקורב לפי משוואה (16):
BW(@VSWR=3) / BW(@VSWR=2) = [(3-1)/√3] / [(2-1)/√2] = 1.63
BW(@VSWR=3) = 3.3 %x 1.63 = 5.4%
בכל הדוגמאות רואים כי הנוסחה המקשרת בין רוחב סרט של VSWR כלשהו לבין רוחב סרט של מחצית ההספק היא קירוב סביר אבל לא מדויק לחלוטין. ניתן לומר כי הנוסחה מגיעה לרמת דיוק מכסימלית עבור אנטנות קטנות שבהן האימפדנס R קבוע בתדר והראקטנס X מתנהג כמו תהודה של סליל וקבל. במקרים שבהם מעגל התמורה מורכב יותר מתקבלות סטיות מן הנוסחה.
מראי מקום
[1] C. A. Balanis, Antenna Theory, Analysis and Design, pp.2-3, Wiley 2005.
[2] C. A. Balanis, Antenna Theory, Analysis and Design, pp.70, 80-85, Wiley 2005.
[3] D. M. Pozar, Microwave Engineering, pp.56-63, Wiley 2012.
[4] Owen Duffy, “Derivation of an expressin for X in terms of VSWR for a normalysed load where R is contant and X changes with frequency” owenduffy.net 26/05/2014.
[5] Owen Duffy, “VSWR curve of a simple series resonant antenna”. owenduffy.net 31/12/2015.
[6] A.D. Yaghjian and S.R. Best, “Impedance. Bandwidth and Q of antennas”, IEEE AP-53, pp. 1298-1323, April 2005.
















