רוחב אלומה והפסד אלומה

1. רוחב האלומה של אנטנה כיוונית

באנטנה כיוונית שהממד הרלבנטי שלה הוא d מתקבלת אלומת קרינה צרה ברוחב זוויתי טיפוסי:

θ ≈ λ/d [radian]

הרוחב הזוויתי המדויק של האלומה תלוי בפונקצית ההארה של המפתח ובשגיאות הפאזה והאמפליטודה על פני האנטנה. פונקציות מישקול ידועות כגון TAYLOR, CHEBISHEV ואחרות, מרחיבות את האלומה אך מקטינות את אונות הצד.

כאשר מציינים את רוחב האלומה בנקודות מחצית ההספק (3 dB) ומשתמשים במעלות במקום בראדיאנים, מקבלים רוחבי אלומה טיפוסיים ואונת צד ראשונה לפי פונקצית המישקול של המפתח כדלקמן [1]-[2]:

מישקול קצה רוחב אלומה אונת צד ראשונה

——————————————————————-

אחיד 50 l/d -13 dB

חלש l/d 60¸55 -15 ¸ -18 dB

חזק 65¸75 l/d -22 ¸ -28 dB

טבלה 1 מישקולים, רוחבי אלומה ואונת צד

2. רוחב האלומה בנקודות הספק שונות

ברוב השימושים המקובלים בתקשורת מסתפקים בידיעת רוחב האלומה בנקודות 3 dB

אך לעיתים יש ענין לדעת מהו רוחב האלומה גם עבור הפסד אלומה אחר. במכ”מי חיפוש נודעת לכך חשיבות מפני שהמטרה לא תמיד נמצאת במרכז האלומה אלא היא “חולפת” על פני האלומה, ולכן נוצר הפסד כלשהו לפי מיקום המטרה על פני האלומה.

איורים 1-3 מדגימים מקרים שונים של רוחבי אלומה, ותמיד ביחס לנקודת רוחב אלומה של מחצית ההספק.

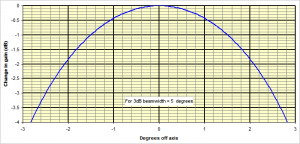
איור 1 עקום קרינה קרטזי של אנטנה, כאשר רוחב האלומה q3dB = 5.0° עיון באיור מראה כי q2dB = 4.2°, q1dB = 3.0°

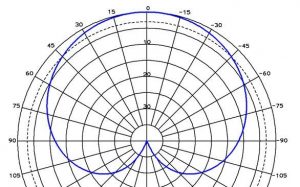
איור 2 עקום קרינה פולרי של אנטנה, כאשר רוחב האלומה q3dB = 90° עיון באיור מראה כי q5dB = 115°, q10dB = 165°

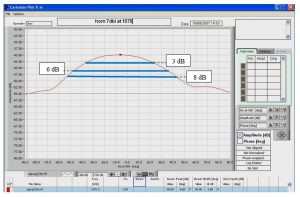
איור 3 עקום קרינה קרטזי של אנטנה, כאשר רוחב האלומה q3dB = 58° עיון באיור מראה כי q6dB = 82°, q8dB = 96°

3. הפסד אלומה גאוסית

מנסיון ממושך עם התמרות פורייה של מפתחים שונים התברר כי עבור רוב הצרכים המעשיים ניתן לקרב את אלומת הקרינה הראשית על ידי אלומה גאוסית כדלקמן :

(2) P(θ) = exp [-k(θ/θ_3dB)²]

θ_3dB היא רוחב האלומה בנקודות מחצית ההספק – דו צדדית

θ היא זווית הסטיה מן המכסימום – דו צדדית

k הוא קבוע נירמול

אם ניקח את המקרה θ / θ_3dB = 1 ונציב P(θ) = 0.5 נקבל k = 0.69

תרשים סכמטי של הזוויות מובא באיור 4.

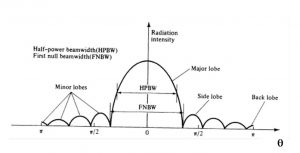
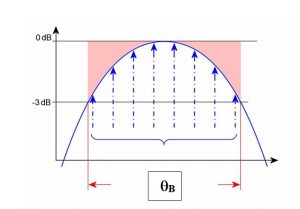
איור 4 תרשים סכמטי של אלומת הקרינה של האנטנה HPBW = Half power beamwidth θ3dB FNBW = First nulls beamwidth θFN » 2.2 θ3dB

נוכל לבטא את נוסחה (2) בעזרת שתי טבלאות מסכמות כדלקמן [3]-[4].

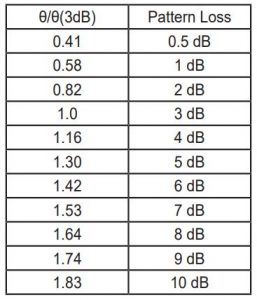
טבלה 2 :רוחב אלומה דו צדדי θמחולק ברוחב אלומה דו צדדי בנקודת 3dB עבור מקרים שונים של הפסד אלומה.

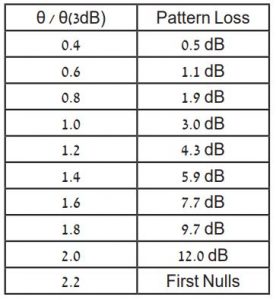
טבלה 3 :הפסד אלומה עבור מקרים שונים של רוחב אלומה דו צדדי מחולק ברוחב אלומה דו צדדי בנקודת 3dB.

4.הפסד אלומה במכ”ם

במכ”ם פולסים, כאשר האלומה חולפת על פני המטרה, פוגעים במטרה מספר פולסים עוקבים, אך כל פולס משודר ונקלט באנטנה במקום אחר על פני האלומה. באינטגרציה של מספר פולסים נוצר הפסד ממוצע הקשור כמובן לצורת האלומה.

בהנחה שמדובר באלומה גאוסית כמתואר במשוואה (2), מספר הפולסים המכסה את רוחב האלומה בנקודות 3 dB הוא n_B ומספר הפולסים הפוגעים באלומה הוא n, הרי ההפסד הנוצר ינתן [5] על ידי ממוצע משוקלל של הפסדי הפולסים הבודדים במשוואה (3).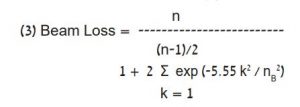

ערכים מעשיים של הפסד האלומה הם 1.6 dB עבור רכבת של 8 פולסים, או הפסד אלומה של 2.0 dB עבור רכבת של 11 פולסים [6]. איור 5 מדגים את השפעת עקום הקרינה על רכבת פולסים [7].