חישובים נומריים הם כלי מרכזי במחקר ובתעשייה. ישנן כיום מגוון שיטות נומריות, שהמשותף להן הוא חלוקת האובייקט שנבחן ל”חתיכות” קטנות (אלמנטים) שלכל אחת מיוחסות התכונות הפיזיקליות הרלוונטיות (למשל, קיבול והולכת חום בבעיות תרמיות, התכונות האוקסטיות בבעיות גלי קול, המקדם הדיאלקטרי לבעיות גלים אלקטרומגנטיים וכו’). במקרים רבים, בפרט, באופטימיזציה של ביצועי התקן\מוצר, נדרשים חישובים חוזרים רבים, לעיתים של היבטים שונים של אותה מערכת, או בשינויים קלים של ההתקן. למשל, בתכנון מערכות אלקטרו-אופטיות, יש לבצע חישובי הארה של התקן אופטי באורכי גל שונים ו\או בזויות שונות על מנת לקבוע את התפלגות השדות האלקטרומגנטיים במרחב לכל צירוף פרמטרים. ככל שההתקן מורכב יותר, מספר האלמנטי הדרוש גדל, כך שזמן החישוב מתארך ומשאבי הזכרון הדרושים גדלים. במקרים רבים, הדבר מטיל מגבלות קשות על התכנון; למשל, הגודל המקסימלי של ההתקן האופטי אותו ניתן לסמלץ בחישוב קטן בהרבה מגודל ההתקן הרצוי. ניתן לרוב להעזר בקירובים, אולם בהרבה מקרים (למשל, כאשר ההתקן מבוסס אלמנטים רבים, או מבוסס אלמנטים השונים מאוד זה מזה בגודלם), הדבר כרוך באי דיוק משמעותי עד כדי אובדן יכולת ניבוי הביצועים.
בניגוד לחישובים הישירים בסגנון הנ”ל, קיימת גישה אלטרנטיבית מבטיחה המבוססת על חישוב ראשוני של האופנים העצמיים (מודים, modes) של המערכת. אם נעזר שוב בדוגמה מעולם האלקטרו-אופטיקה, בגישה זו ניתן להמנע מביצוע סימולציות חוזרות בזויות הארה שונות על ידי כיבוי מקור האור וניסוח הבעיה כך שפתרונותיה יתארו את כל התפלגויות השדות האלקטרומגנטיים הנתמכות על ידי ההתקן. מתימטית, מדובר בהחלפת בעיית הפיזור (שצורתה Ax=b; A מתאר את הפיזיקה הרלוונטית, כלומר משוואות מקסוול, b את מקור האור ו- x את הפתרון) בבעיית ערכים עצמיים (שצורתה Ax=vx). במקרה זה, יש אינסוף פתרונות למודים ולפונקציות העצמיות (v ו- x בהתאמה), אך לרוב, ניתן להגיע לדיוק מספק על ידי כתיבת הפתרון לבעיה הכללית עם מספר מצומצם יחסית של אופנים.
הקושי בגישה זו הוא כפול. ראשית, עד לאחרונה לא היה ברור כיצד לקשר בין הפתרון של הבעיה הכללית (שבה המקור b, דהיינו, פרטי ההארה, מוגדר) לבין האופנים העצמיים עבור מערכות שבהן חלק מהאנרגיה אובדת בשל בליעה או בשל פיזור מחוץ לתחום העניין. עבור הבעיה האלקטרומגנטית, קושי זה הוסר במאמר שבו הראינו שניסוח עם סוג מיוחד של אופנים עצמיים (שהערך העצמי שלהם מתאר את המקדם הדיאלקטרי של ההתקן, או של חלקים ממנו) מאפשר לקבל ניסוח מדוייק ושלם של הקשר בין הבעיה הכללית ובעיית הערכים העצמיים תוך שימוש באופנים עצמיים שאינם מתבדרים במרחב; בכך, עקפנו את הקשיים המתימטיים המרובים שהיו כרוכים בפתרון ששימש את קהילת החוקרים של הבעיה עד כה.
הקושי השני הוא בחישוב האופנים העצמיים בדיוק, מהירות ואמינות גבוהים. אמנם, חישוב נומרי של האופנים אפשרי בתוכנות מסחריות נפוצות, אבל הוא לרוב איטי מאוד, מחסיר אופנים חשובים, ומייצר אופנים רבים שמשקלם זניח וחלקם אף שגויים מיסודם . גם לקושי זה אנו מציעים פתרון יעיל. בפרט, בהשראת תורת הפרעות ממכניקה קוואנטית, אנחנו יכולים לכתוב את האופן של אובייקט מסובך כסכום ממושקל של אופנים של אובייקט פשוט (כדוגמת כדור, גליל או שכבה) אותם ניתן לחשב בקלות יחסית, כלומר
שוב, אנו מתמקדים כאן בבעיה האלקטרומגנטית. בהצבת הפתרון הזה במשוואות הרלוונטיות (מקסוול), מתקבלת משוואת ערכים עצמיים שיחודה הוא שבניסוח מטריצי, גודלה קטן משמעותית (לעיתים בסדרי גודל) מגודל המטריצות שבהן יש לטפל בניסוח הרגיל. כפועל יוצא, זמני הריצה הדרושים קצרים בהרבה. לדוגמה, ב- [2] הדגמנו שחישוב האופנים של מפזר אור אליפטי (ראה תמונה 1 (a)) מדוייק מאוד ומהיר מאשר בתוכנת חישוב מסחרית באופן משמעותי; ניתן לראות את קצב ההתכנסות בתמונה 1 (b). נציין שהגישה שלנו כוללת משפחה יחודית של אופנים שמאפשרת לטפל בשינויים חדים בגיאומטריה עם מספר קטן יחסית של אופנים שמשחזרים בנאמנות את השינוי הנ”ל.
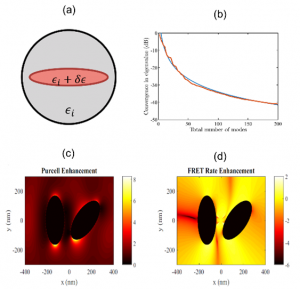
תמונה 1. (a) תרשים סכימטי של מפזר אליפטי שהאופנים העצמיים שלו מחושבים מתוך האופנים של מפזר כדורי והפונקציה המרחבית המתארת את ההפרעה במקדם הדיאלקטרי . (b) קצב ההתכנסות של חישוב ערך עצמי של אופן של המפזר האליפטי . (c)-(d) מיפוי מקדמים הגברת פליטת אור והעברת אנרגיה (בהתאמה) מזוג מפזרים אליפטיים, המחושבת על בסיס שימוש באופנים של מפזר יחיד . התמונות מופיעות באישור.
אחד מיתרונותיה הגדולים של הגישה שלנו היא היכולת לטפל במספר גדול של אובייקטים מבלי לסבול מהאטה דרסטית של זמן החישוב וללא הזדקקות למשאבי חישוב לא ריאליים. בפרט, בגישה שלנו אין קושי מיוחד לטפל באובייקטים שהם מאוד שונים בגודלם. עבור מערכת של זוג מפזרים אליפטיים, הדגמנו שמיפוי קצב פליטת אור מפולטים קוואנטיים שמוצבים בסמוך מהיר פי 1000 מאשר בתוכנת חישוב מסחרית (ראה תמונה 1 –(d)(c)). הדגמת יעילות החישוב למערכות גדולות יותר מתבצעת בימים אלו, למשל, עבור תכנון מטא-משטחים בגודל של מאות מיקרונים.
הגישה שלנו מומשה גם לתכנון סיבים מודרניים (כאלו שאינם מבוססים על החזרה פנימית מלאה, כגון סיבי חלולים שמיועדים להולכת אור באוויר), לאובייקטים בעלי מקדמים אופטיים לא אחידים ולא איזוטרופיים, מערכות מחזוריות , וכן לטיפול באפקטים קוואנטיים קשים לחישוב כגון פליטה תרמית ופלורסצנציה . ניתן גם לחשב את התגובה הספקטרלית על בסיס דגימה יחסית דלילה בדיוק טוב; הביצועים בדוגמה פשוטה היו שקולים לאלו שהתקבלו בעזרת תוכנה מסחרית .
לאחר ההדגמות הללו של מהירות החישוב בגישה שלנו, הכוונה היא להתממשק לאלגוריתמים של אופטימיזציה ולמידת מכונה על מנת לאפשר תכנון מהיר ויעיל מאשר מתבצע כיום. לסיום, שווה לציין שבעוד שהעבודה שביצענו עד כה התמקדה בבעיות אלקטרומגנטיות, האלמנטים החדשניים שלנו יכולים להיות מותאמים לבעיות פיזיקליות אחרות, כגון לגלים אקוסטיים, בעיות חום ולחץ, ואף לישומים של תאורה בגרפיקה ממוחשבת, הדפסה תלת מימדית וכו’.
















