מטרת מאמר זה היא לתאר ולנתח מנוע אלחוטי המבוסס על שדות אלקטרומגנטיים מושהים. החוק השלישי של ניוטון קובע שכל פעולה מאוזנת על ידי תגובה בגודל שווה אך בכיוון הפוך. הכוח הכולל במערכת שאינה מושפעת מכוחות חיצוניים הוא אפס. עם זאת, על פי עקרונות תורת היחסות אות לא יכול להתפשט במהירויות העולות על מהירות האור. מכאן שהפעולה לא יכולה להיווצר בו-זמנית עם התגובה, ולכן הכוח הכולל לא יכול להיות בטל בכל זמן נתון. במאמר קודם [1] הראינו שהחוק השלישי של ניוטון אינו יכול להתקיים בדיוק במערכת מבוזרת שהחלקים השונים שלה נמצאים במרחק סופי זה מזה. זה נובע מהמהירות הסופית של התפשטות אות שאינה יכולה לחרוג ממהירות האור בוואקום, מה שגורם לכך שכאשר מסכמים את הכוח הכולל במערכת הכוח אינו מסתכם באפס. זה הוכח בדוגמה ספציפית של שתי לולאות זרם עם זרמים תלויי זמן, הניתוח לעיל הוביל להצעה של מנוע יחסותי [2, 3]. מכיוון שהמערכת מושפעת על ידי כוח כולל לפרק זמן מוגבל, המשמעות היא שהמערכת רוכשת תנע ואנרגיה מכאניים, נשאלת השאלה כיצד נוכל להכיל את חוק התנע ושימור האנרגיה. נושא שיחת המומנטום נדון ב-[4], בעוד שתוצאות לגבי שימור אנרגיה נדונו ב-[5, 6, 7,9]. ניתוח קודם הסתמך על העובדה שהגופים היו טבעיים מבחינה מקרוסקופית, כלומר מספר האלקטרונים והיונים שווה בכל אלמנט נפח. במחקרים מאוחרים יותר אנו נמנעים מהנחה זו וחוקרים גופים טעונים [,1610,11,12,13,14,15] המקיימים אינטראקציה עם זרמים מגנטיים הנישאים על ידי חומרים מגנטיים קבועים, ובכך מנתחים את ההשלכות על מנוע אלחוטי אפשרי המבוסס על מגנט קבוע.
מָבוֹא
מערכות ההנעה של ימינו מבוססות על שני חלקים חומריים שכל אחד מהם מקבל תנע שווה והפוך לתנע שצובר החלק השני. דוגמה טיפוסית לסוג זה של מערכת היא רקטה שפולטת גז כדי להניע את עצמה. עם זאת, השיקולים היחסותיים לעיל מצביעים על סוג חדש של מנוע שבו המערכת אינה מורכבת משני גופים חומריים אלא מגוף חומרי ושדה. התעלמות מהשדה צופה נאיבי יראה את הגוף החומרי צובר תאוצה שנוצרה יש מאין, עם זאת, צופה בעל ידע יבין שכמות המומנטום ההפוכה מתקבלת על ידי השדה כפי שהוצג ב-[4]. אכן המשפט של Noether מכתיב שכל מערכת שיש לה סימטריה להזזה מרחבית תשמור על התנע הקווי והמערכת הפיזית הכוללת חומר ושדה היא אכן סימטרית להזזה, בעוד שכל תת-מערכת (בין אם היא חומר או שדה) לא. תוצאה זה תוארה כבר על ידי פיינמן [8]. פיינמן מתאר שני מטענים הנעים אורתוגונלית, שמפרים את החוק השלישי של ניוטון שכן הכוחות שהמטענים מעוררים זה על זה אינם מבטלים (חלק אחרון של 26-2), הפרדוקס הזה נפתר ב- (27-6) שבו מוצג כי התנע שנצבר על ידי מערכת שני המטענים מאוזן על ידי התנע של השדה.
המנוע היחסותי
נגדיר מנוע יחסותי כמערכת פיזיקלית שמרכז המסה שלה בתנועה עקב האינטראקציה של חלקיו החומריים. חלקים אלה עשויים להיות חופשיים לנוע אחד ביחס לשני או מוחזקים באופן מעשי יותר במסגרת נוקשה. אין לכך שום חשיבות שכן אנו מתעניינים רק בתנועת מרכז המסה בעבודה זו. נדגיש כי מנוע יחסותי מאפשר תנועה של 3 צירים (כולל אנכית), אין לו חלקים נעים, יש לו צריכת דלק אפסית (ולכן אפס פליטת פחמן) והוא זקוק רק לאנרגיה אלקטרומגנטית אשר עשויה להיות מסופקת על ידי פאנלים סולאריים. המנוע היחסותי הוא פתרון אידיאלי למסעות בחלל כאשר כיום חלק גדול ממסת רכב החלל מוקדש לדלק.
במאמר [10] הוכחו שני הנוסחאות החשובות בתורת המנועים היחסותיים: זאת המתייחסת לכוח שנוצר במרכז המסה של המערכות וזאת המתייחסת לתנע הכולל של המערכת:
אנו רואים כי המנוע היחסותי יכול גם להגיע למצב סטציונרי שבו המטענים והזרמים אינם תלויים בזמן, וכמובן יכולים להתקיים מנועים שבהם התנועה מותנה בשינוי מתמשך בזמן של הזרמים והמטענים במערכת. כמו כן המערכת תלויה בצפיפויות המטענים והזרמים, כאשר יש יתרון מובהק לצפיפות מטען גבוהה לצורך קבלת כוחות ומהירויות רלבנטיים טכנולוגיים. יחד עם זאת צפיפות מטען גבוהה מדי עלולה להוביל לשדה חשמלי גבוה שהוא מעל ומעבר לחוזק הדיאלקטרי של החומר ולכן לפריצה חשמלית שתאיין את המטען שנצבר. הפתרון לכך יכול להסתמך על צפיפויות המטען הגבוהות שקיימות ברמה האטומית של החומר ומניפולציה שלהם [11,12], יחד עם זאת ניתוח של הדינמיקה ברמה זו דורשת שימוש בכלים של הפיזיקה הקוואנטית ולא ניתן להסתפק בניתוח קלאסי [13].
דוגמאות
להלן מספר מימושים של מנוע יחסותי. במאמר [10] מתואר מנוע המבוסס על קבל טעון וכריכת זרם:
נוסחא 1
נוסחא 2
ניתן להחליף את כריכת הזרם במגנט קבוע [15] ולקבל מימוש נוסף:
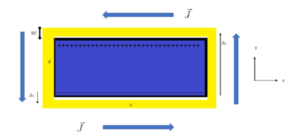
איור :1 דוגמא למנוע יחסותי טעון המטענים החיוביים מתוארים על ידי הסימן + והשליליים
על ידי הסימן .- האיור לעיל מתאר חתך של המנוע, הצבע הצהוב מתאר כריכת זרם כאשר כיוון
הזרם מתואר על ידי החיצים.
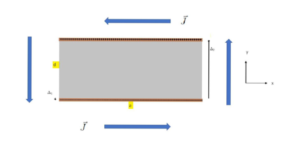
איור 2: דוגמא למנוע יחסותי טעון המטענים החיוביים מתוארים על ידי הסימן + והשליליים על ידי הסימן -. האיור לעיל מתאר חתך של המנוע, הצבע האפור מתאר מגט קבוע כאשר כיוון זרם המיגנוט (הרוטציונל של המגנטיזציה) מתואר על ידי החיצים.
פתרון נוסף קיים גם במערכת שבה הזרמים והמטענים משתנים בצורה מחזורית בזמן ואינם מגיעים לערך קבוע [16], במקרה זה ניתן להראות שזרימה מחזורית בשני מקטעי זרם בהפרש פאזה של תשעים מעלות, תייצר תנע לינארי כולל:
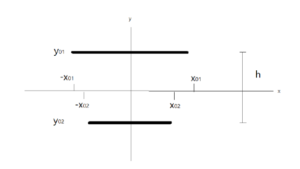
איור 3: דוגמא למנוע יחסותי טעון המורכב משני מקטעי חוט מוליך, המטען עובר באופן מחזורי בין קצוות החוטים, כאשר הקצוות טעונים לערכם המקסימלי המטען זורם בכיוון ההפוך עד שמגיעים לערך המינימלי שהוא המטען ההפוך בסימנו לערך המקסימלי.
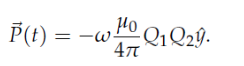
במקרה זה מקבלים משוואת תנע פשוטה מהצורה:
אפשר לראות שכדי לקבל מנוע המתאים לרכב נוסעים בעל משקל של טון אחד, נדרשים הפרמטרים הבאים שהם קשים מאד להשגה:
| Quantity | Value | Units | Value | Units |
| f | 1 | GHz | ||
| Q1 | 10 | Coulomb | ||
| Q2 | 10 | Coulomb | ||
| m | 1000 | kg | 1 | ton |
| P | 62800 | kg m/s | ||
| v | 63 | m/s | 226 | km/h |
נראה שברמה המקרוסקופית קשה מאד לקבל מנוע יחסותי שהוא משמעותי מבחינה טכנולוגית. הפתרון המסתמן הוא מניפולציה של החומר ברמה האטומית\כימית ועל כך ניתן לקרוא במאמרים [11,12,13].

פרופסור אשר יהלום
קרדיט: דוברות אוניברסיטת אריאל










