- קיטוב של גל אלקטרומגנטי
קיטוב (polarization) הוא תכונה כללית של גל אלקטרומגנטי המתפשט במרחב ומשמעותה היא הכיוון של וקטור השדה החשמלי בתלות בזמן [1]-[4]. היות וגל אלקטרומגנטי במרחב משודר ונקלט על ידי אנטנות כלשהן הרי ניתן לייחס את תכונת הקיטוב של הגלים במרחב לאנטנות עצמן.
נתאר את השדה החשמלי המשודר או נקלט באנטנה כלשהי כסכום וקטורי של שני שדות ניצבים זה לזה Ex, Ey:
(1) E = [1x Ex + 1y Ey] exp (jwt)
1y, 1x הם וקטורי יחידה בצירים x,y ואילו Ex, Ey הם השדות החשמליים בכיוונים x,y.
הקיטוב הוא קו דמיוני במרחב המוכתב על ידי קצה הוקטור החשמלי. הקיטוב מאונך לכיוון השדה המגנטי ולכיוון ההתפשטות. למעשה, הקיטוב הכללי ביותר הוא אליפטי, אך אם ציר אחד קטן מאד ביחס לציר השני, הקיטוב הוא לינארי.
- קיטוב ניצב
קיטוב לינארי מושלם בכיוון x מתקבל אם Ey=0 וקיטוב לינארי מושלם בכיוון y מתקבל אם Ex=0. באופן מעשי נוח להגדיר קיטוב אנכי וקיטוב אופקי, אך אלו הן הגדרות הקשורות להצבה המרחבית של האנטנה ולא לתכונת הקרינה הבסיסית שלה. במקרה שבו האנטנה היא אלמנט זרם אנכי (כגון: דיפול או מונופול) או אלמנט שדה אנכי (כגון: קצה גלבו או אלמנט מיקרוסטריפ) נאמר שהאנטנה משדרת או קולטת בכיוון אנכי, אבל ברור שאם נסובב את האנטנה סביב ציר הקרינה ב-90 מעלות אזי הקיטוב שלה יהיה אופקי. אנו מבינים אפוא שלאנטנה יש קיטוב לינארי, אך כאשר מציבים את האנטנה במרחב מתקבלת הבחנה בין קיטוב אנכי לבין קיטוב אופקי.
היחס בין ההספק הנקלט באנטנה לינארית בקיטוב ניצב ((cross-pol לבין ההספק הנקלט בקיטוב הראשי ( (co-polנקרא “קיטוב ניצב” cross polarization [5] כמודגם באיורים 1-4. ברוב המקרים מעונינים שהקיטוב הניצב יהיה בעל ערך קטן ככל האפשר, למשל אם בכל קיטוב מועבר מידע אחר. בכתבה זו נציג שיטת מדידה מקובלת למציאת ערכו של הקיטוב הניצב.

איור 1: עקומי קרינה של אנטנה בשני קיטובים: קיטוב ראשי copolar בצבע כחול וקיטוב ניצב crosspolar בצבע אדום. היחס בין הגרף האדום והגרף הכחול בכל זווית נתונה הוא הערך המדוד של הקיטוב הניצב (ביחידות dB).
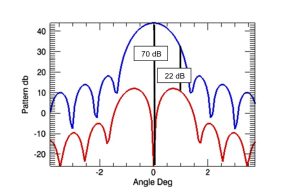
איור 2: עקומי קרינה של אנטנה בשני קיטובים: קיטוב ראשי copolar בצבע כחול וקיטוב ניצב crosspolar בצבע אדום. הקיטוב הניצב בזווית 00 הוא כ- -70 dB ובזווית 10 הוא כ- -22 dB
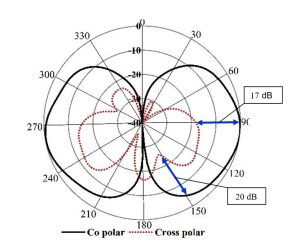
איור 3: עקומי קרינה של אנטנה בשני קיטובים: קיטוב ראשי copolar בצבע שחור וקיטוב ניצב crosspolar בצבע אדום, בהצגה פולרית. הקיטוב הניצב בזווית 900 הוא כ- -17 dB ובזווית 1500 הוא כ- -20 dB
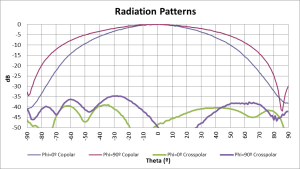
איור 4: עקומי קרינה של אנטנה בשני חתכים ראשיים phi=00, phi=900 בקיטוב ראשי copolar ובקיטוב ניצב .crosspolar בחתך phi=900 רוחב האלומה הוא 800 והקיטוב הניצב בתוך האלומה הראשית מגיע עד -35 dB בחתך phi=00 רוחב האלומה הוא 600 והקיטוב הניצב בתוך האלומה הראשית מגיע עד -40 dB
- שיטת המדידה של קיטוב ניצב
נציב אנטנת שידור לינארית בצד אחד של המטווח ואנטנת קליטה נבדקת בצד השני של המטווח. נמדוד עקום קרינה בצידוד או בהגבהה, פעם אחת כאשר אנטנת השידור מקוטבת אנכית ופעם שניה כאשר אנטנת השידור מקוטבת אופקית כמתואר באיור 5 לפי 5] – [7]].

איור 5: סכימה של מדידת הקיטוב הניצב
דוגמאות נוספות של חתכי קרינה בשני קיטובים מובאות באיורים 6-8. איור 6 מראה עקום קרינה של אנטנת צלחת לווינית בקוטר 3 מטר עם מספר רב של אונות צד. הקיטוב הניצב בזווית 0° הוא בסביבות -90 dB כלומר ערך נמוך ברמה יוצאת דופן.
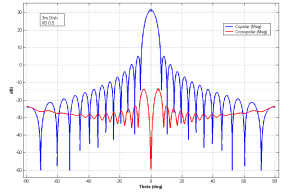
איור 6: חתכי קרינה בקיטוב ראשי ובקיטוב ניצב של צלחת פרבולית עם קיטוב ניצב נמוך במיוחד. קרדיט [8].
איורים 7-9 מראים חתכי קרינה של אנטנת מיקרוסטריפ דו-קיטובית (מוזנת בשנתי נקודות אורתוגונליות) עם גירסאות שונות של נקודת ההזנה.
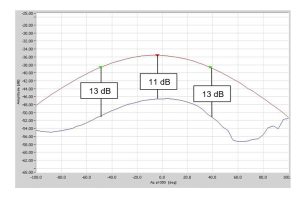
איור 7: חתכי קרינה בקיטוב ראשי ובקיטוב ניצב של אלמנט מיקרוסטריפ (הזנה בגירסה ראשונה). הקיטוב הניצב בתוך האלומה הראשית הוא dB -11
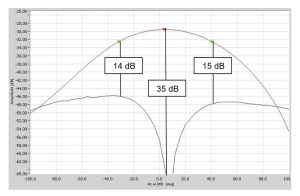
איור 8: חתכי קרינה בקיטוב ראשי ובקיטוב ניצב של אלמנט מיקרוסטריפ (הזנה בגירסה שניה). הקיטוב הניצב בתוך האלומה הראשית הוא -14 dB
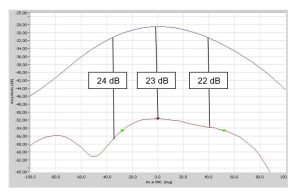
איור 9: חתכי קרינה בקיטוב ראשי ובקיטוב ניצב של אלמנט מיקרוסטריפ (הזנה בגירסה שלישית). הקיטוב הניצב בתוך האלומה הראשית הוא -22 dB
רואים ששינוי בנקודת ההזנה משפיע על הקיטוב הניצב באופן ניכר.
- דיוק המדידה
דיוק המדידה תלוי בעיקר ברמת ה”נקיון הקיטובי” של אנטנת השידור. נניח שהקרינה בשתי האנטנות מתפצלת לשני וקטורים מאונכים זה לזה. אנטנת השידור מקרינה הספק a בכיוון y והספקb בכיוון x. אנטנת הקליטה קולטת הספק c בכיוון y והספק d בכיוון x כמתואר באיור 10.
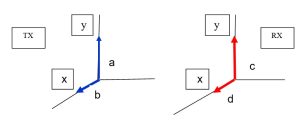
איור 10 : ההספקים המוקרנים והנקלטים בשתי האנטנות
הקיטוב הניצב של אנטנת השידור הוא b/a
(2) Cross polarization of TX = b/a
הקיטוב הניצב של אנטנת הקליטה הוא d/c
(3) Cross polarization of RX = d/c
ההספק a עובר אל c ואינו עובר ל-d ואילו ההספק b עובר אל d ואינו עובר ל-c
מכאן שההספק הנקלט יהיה ac+bd
כעת נגלגל את המשדר ב-90 מעלות כמתואר באיור 11.
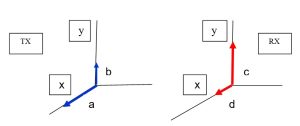
איור 11 : ההספקים המוקרנים והנקלטים בשתי האנטנות לאחר גלגול
ההספק a עובר אל d ואינו עובר ל-c
ההספק b עובר אל c ואינו עובר ל-d
מכאן שההספק הנקלט יהיה ad+bc
רמת הקיטוב הניצב הנמדדת תהיה
ad + bc
(4) Measured cross = ————
ac + bd
כדי שהמדידה תהיה מדויקת, צריך לדאוג לכך שרמת הקיטוב הניצב של אנטנת השידור תהיה נמוכה משמעותית מרמת הקיטוב הניצב של אנטנת הקליטה (הנבדקת). אחרת, לא נדע אם הקיטוב הניצב שייך לאנטנה הנבדקת או לאנטנה המשדרת.
דוגמאות מספריות (נזכור להציב במשוואה 4 ערכים ממשיים ולא דציבלים, למשל במקרה הראשון a=1.0 , b=0.1 , c=1.0 , d=0.1 והתוצאה cross = 0.2/1.01 = 0.198
TX cross RX cross measured cross
-10 dB -10 dB -7.0 dB
-20 dB -10 dB -9.6 dB
-30 dB -10 dB -9.9 dB
-20 dB -20 dB -17 dB
-30 dB -20 dB -19.6 dB
כדי לדעת בצורה מהימנה מהו הקיטוב הניצב של אנטנת השידור נעדיף לבצע קודם כל מדידה של שתי אנטנות שידור זהות ולחלץ את הקיטוב הניצב המדויק של אנטנת השידור (הוא יהיה נמוך ב-3dB מהערך המדוד של הכיול). אחר כך נשתמש בערך זה כדי למדוד את האנטנה הנבדקת האמיתית. טכניקה זו זכתה לשם three antennas cross polarization [9]-[12].
מראי מקום
[1] R.S. Elliott, Antenna Theory and Design, John Wiley, 2003.
[2] C.A. Balanis, Antenna Theory – Analysis and Design, Wiley 2015.
[3] J.D. Kraus and R.J. Marhefka, Antennas, McGraw Hill, 2001.
[4] S. Gao, Q. Luo and F.Zh, Circularly Polarized Antennas, J. Wiley and sons, 2014.
[5] A. Ludwig, “The Definition of Cross Polarization”, IEEE Trans. AP-21, pp. 116-119, 1973.
[6] A. Newell, R. Baird, P. Wacker, “Accurate Measurement of Antenna Gain and Polarization at Reduced Distances by an Extrapolation Technique”, IEEE Trans. AP-21, pp. 418-431, 1973.
[7] E.B. Joy, D.T. Paris, “A Practical Method for Measuring Complex Polarization Ratio of Arbitrary Antenna”, IEEE Trans. AP-21, pp. 432-435, 1973.
[8] R. Galuscak and P. Hazdra, Circular Polarization and Polarization Losses CTU Prague, FEE, Dept. of Electromagnetic Field, Technicka 2, 166 27, Prague, Czech Republic, E-mail:, om6aa@yahoo.com, hazdrap@fel.cvut.c
[9] A. Newell, “Improved Polarization Measurements Using a Modified Three Antenna Technique”, IEEE Trans. AP-36, pp. 852-854, 1988.
[10] Watkins Johnson Tech-Notes, Antenna polarization, V6-4.
[11] Watkins Johnson Tech-Notes, Polarization measurements 1, V14-1.
[12] Watkins Johnson Tech-Notes, Polarization measurements 2, V15-1.


