עם הכניסה של המידול הגיאומטרי הממוחשב לשימוש מסיבי, בשנות השישים של המאה הקודמת, הייצור של עצמים מלאכותיים ידע עדנה. כל מכונית או מטוס, פלאפון או רחפן נבנים תחילה גיאומטרית במחשב, עוברים אנליזות ואופטימיזציות ממוחשבות, ואף מיוצרים בעזרת מחשב. ועם זאת, מהפכת המידול הגיאומטרי אשר איתנו כבר יותר מחצי מאה, עברה מעט מאד שינויים בתקופה זו. הייצוג הבסיסי של משטחי ספליין פרמטריים למקוטעין (trimmed parametric spline surfaces) הומצא לפני כחמישים שנה כייצוג של שפת המודל (Boundary-representation or B-rep) והוא עדיין הייצוג הכמעט בלעדי בכל מערכות התיב”ם (תכנון ויצור בעזרת מחשב) המכאני כיום.
מספר תהליכים בעשור האחרון דוחפים שינוי. תהליכי האנליזה, מעצם מהותם, תמיד היו נפחיים, מה שחייב מעבר מ-B-rep לייצוג ניפחי של המודל בזמן האנליזה, למשל כ Finite Elements (FE). מרחבי ה-B-rep וה-FE לא תואמים והמעברים ביניהם לא טריוויאליים. לא ממודל ה-B-rep ל-FE נפחי וגם לא חזרה, כשתוצאות האנליזה אמורות להיות ממופות חזרה למודל ה-B-rep. המודל ה-B-rep מגדיר את מעטפת המודל ואפשר את הייצור בכרסום של עובד הומוגני – אלומיניום או פלדה וכו’. מאידך, תהליכי יצור מודרניים, ביחוד בתחום הדפסת התלת מימד או היצור התוספתי (Additive manufacturing or AM), מאפשרים הטרוגניות בחומר אשר משתנה בתוך המודל (Functionally graded materials , or FGM) ומערכות התיב”ם המודרניות לא תומכות ביכולות אלו. לא בזמן המידול, לא לצרכי אנליזה וכמובן לא תומכות ביצור של חלקים הטרוגניים.
מסיבות אלו, מערכות המידול הגיאומטרי חייבות לעבור שינוי בסיסי בייצוג. B-rep המבוסס על משטחי ספליין לא מספק עוד. פתרון אחד המבוסס על ווקסלים (voxels) מאפשר הטרוגניות בתוך הגוף אבל הוא גם בעל חסרונות לא מועטים. הייצוג לא תומך בצורות חופשיות (freeform shapes), לא תואם את ייצוגי הספליין המקובלים והוא לא מדויק כשדיוק סביר מומר לסדרי גודל זיכרון שגם מחשבים מודרניים לא מסוגלים להכיל.
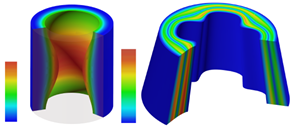
תמונה 1 :שני מודלים הטרוגניים של דלק רקטי מוצק הכוללים מאיצי בערה (באדום) ומאיטי בערה (בכחול). קרדיט: © גרשון אלבר, מדעי המחשב, טכניון
במהלך העשור האחרון, אנחנו מפתחים בטכניון מנוע גיאומטרי מבוסס על ייצוגי ספליין פרמטריים נפחיים למקוטעין (trimmed parametric spline trivariates) ואשר נותן מענה לקשיים המתוארים ויותר, ייצוג הקרוי V-rep עבור Volumetric representation. המעבר ממשטחי ספליין לנפחי ספליין (trivariate splines) נותן שליטה מלאה על כל נפח המודל כולו ומאפשר לכן ייצוג של הטרוגניות בכל מימד. במילים אחרות, ניתן לקודד שדות סקלרים, וקטוריים או טנזוריים בתוך נפח המודל. לכל נקודה פנימית במודל יהיו, בהתאמה, ערכים של שדות סקלרים, וקטוריים או טנזוריים וללא כל מגבלה. תמונה 1 מציגה שני מודלי V-rep הטרוגני של דלק רקטי מוצק בעלי גיאומטריה כללית והמכילים מאיטי בערה ומאיצי בערה כדי לשלוט על פרופיל הבערה בזמן של המנוע הרקטי. ההטרוגניות במודלים אלו מיוצגת על ידי צבע.
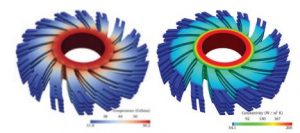
תמונה 2 :מימין מוצג מודל rep-V של גוף קירור ל LED אשר מכיל חומרים בעלי מקדם הולכת חום משתנה (FGM)משמאל, תוצאת Analysis Geometric-Iso לחישובי מעבר החום. בשיתוף פעולה עם Buffa Annalisa and Antolin Pablo (EPFL.) קרדיט: © גרשון אלבר, מדעי המחשב, טכניון
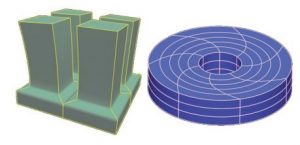
תמונה 3 :המודל הגלובלי (מקרו) מימין ומודל האריח (מיקרו) משמאל, הם כל שנדרש על מנת להגדיר את המודל שנראה בתמונה 2. קרדיט: © גרשון אלבר, מדעי המחשב, טכניון
בנוסף, מעצם היותו נפחי, מודל ה-V-rep הופך את הקישוריות לשלבי האנליזה והאופטימיזציה לפשוטים הרבה יותר. עובדה זו משתלבת מיידית עם תחום אנליזה חדש אשר מתפתח בעשור האחרון והוא אנליזה מבוססת ספליינים. במילים אחרות אותו הייצוג בשלבי התכנון, משמש מיידית וללא כל המרה גם בשלבי האנליזה, הליך שמייתר כל צורך במיפויים בין מרחבים. התחום, באופן לא מפתיע, נקרא Iso-Geometric Analysis (IGA) שמרמז על ייצוג גיאומטרי אחוד גם בשלבי התכנון וגם בשלבי האנליזה. ייצוג ה-V-rep של הספליין הנפחי מתאים מיידית גם ל IGA. תמונה 2 מציגה גוף קירור עם מקדם מעבר חום משתנה (הטרוגני) ואשר עבר אנליזת IGA ישירות ממודל ה V-rep- המתוכנן.

תמונה 4 :ארבעת הכנפיים מימין שונות זו מזו בדיהדרל שלהן למרות כוח העילוי הזהה שמופעל עליהן בכל ארבעת המקרים. הגיאומטריה של אריחים שונה במקומות שונים, כאשר כל האריחים באים ממשפחה רציפה עם מספר פרמטרים כשמספר דוגמאות מוצגות משמאל. Analysis Geometric-Iso בשיתוף פעולה עם Buffa Annalisa and Antolin Pablo (EPFL.) קרדיט: © גרשון אלבר, מדעי המחשב, טכניון
במקומות שונים, כאשר כל האריחים באים ממשפחה רציפה עם מספר פרמטרים כשמספר דוגמאות מוצגות משמאל. Iso-Geometric Analysis בשיתוף פעולה עם Pablo Antolin and Annalisa Buffa (EPFL).
לייצוג ה-V-rep הניפחי ישנה יכולת משמעותית אחרת, שתמונה 2 כבר מרמזת עליה. למרות שתמונה 2 מייצגת גוף סריגי (Lattice) מורכב ועם שטח פנים גדול (כנדרש מגוף קירור), הגוף הוגדר בעזרת שתי גיאומטריות בסיסיות בלבד ואשר מוצגות בתמונה 3. האחת, מקרו, מגדירה את התצורה הגלובלית של המודל והשניה, מיקרו, מגדירה את הגיאומטריה של האריח. העובדה שקיימת פונקציית V-rep נפחית פרמטרית (המקרו) אשר מכסה את כל נפח המודל מאפשרת לנו למפות אריחים(tiles) בדידים לתוכה בעזרת הרכבה פונקציונלית (functional composition), ישירות מעל מרחבי ספליין. אם המקרו הינו ספליין M והמיקרו הינו ספליין m, אזי ההרכבה המתמטית של M(m) מיפתה את m דרך M. בעזרת מיפוי של קבוצה גדולה של אריחים, mi, הממוקמים האחד בצמוד לשני בתחום של M, ניתן ליצור סריג גאומטרי שלם אשר עוקב אחרי צורת המקרו M עם אריחים ממופים M(mi), מההרכבה על M. יתרה מזאת, האריחים יכולים לשנות את צורתם במקומות שונים במודל או את הרכב החומר ממנו הם עשויים. במילים אחרות הסריג יכול להיות הטרוגני בהרכב החומרים שלו ו\או בגיאומטריה של אריחיו.
כך לדוגמה, תמונה 4 מציגה סריג של כנף אשר תוכנן עם אריחים המשתנים בצורתם לאורך הכנף (כמובן כאשר הרציפות של כל גיאומטרית הכנף נשמרת). למרות שבכל ארבעת האנליזות שבתמונה 4 תנאי השפה זהים (כוח עילוי על כל השטח התחתון של הכנף שמעוגנת בשורשה). הכיפוף או הדיהדרל של הכנפיים שונה בגלל הגיאומטריה השונה של אריחים מסוימים בכנפיים השונות.
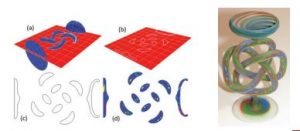
תמונה 5 :משמאל, במקום חתך (b) של מודל rep-B (a) המייצג את קו המתאר של המודל (c) חתך rep-V מיוצג כתמונה (d)כשכל צבע מייצג סוג חומר בתוך המודל, בחתך זה. מימין, המודל שהודפס במדפסת של Stratasys בעזרת VoxelPrint קרדיט: © גרשון אלבר, מדעי המחשב, טכניון
עד כה דיברנו על V-rep בשלבי תכנון ואנליזה. מה לגבי הדפסת תלת מימד? אם הדפסת תלת מימד קלסית דורשת חתכים אופקיים (slices) של מעטפת המודל, כדי להדפיס גוף הטרוגני נדרשת גם ההגדרה של סוג חומר, בכל נקודה בתוכו. פתרון אחד אפשרי מוצע כיום על ידי חברת Stratasys והוא VoxelPrint. במקום חישוב חתך מישורי של מודל הB-rep המייצר את קווי-המתאר של הגוף, החתך מוחלף בתמונה צבעונית כשהצבע בכל פיקסל בתמונה מייצג סוג חומר אחד בנקודה זו, בגובה החתך. תמונה 5 מראה דוגמה אחת. במקום חתך קווי-מתאר אשר מפריד בין פנים לחוץ המודל (תמונה 5 (c)), להדפסת מודל הטרוגני כמו בתמונה 5 מימין, נדרשות אלפי תמונות (חתכים) כשכל חתך הוא תמונה על עשרות מיליוני פיקסלים (תמונה 5 (d))! יש לציין שהגיאומטריה הרציפה והחלקה של מודל ה-V-rep, של כמה מגה בייט, הומרה למאות מגה-בייט של תמונות דיסקרטיות לצרכי הדפסה בלבד ולצרכי הממשק שהמדפסת מציעה.
יכולת נוספת שמתאפשרת בסריגים בעזרת V-rep היא סגור רקורסיבי. אם ההרכבה של אריחי mi, בתחום של M יצרה microstructure lattice אזי שימוש בכל אחד מן האריחים בתוצאה M(mi) כגוף מקרו חדש ייצור nanostructure lattice וחוזר חלילה. הסרטון https://youtu.be/u-A_HrqvkGU מדגים יכולת זו. לסיום, תמונה 6 מציגה מספר מודלים הטרוגניים ופורוזיביים אשר הודפסו על ידי מדפסות תלת מימד.

» תמונה 6 :מספר מודלים rep-V הטרוגניים ו\או פורוזיביים אשר הודפסו במדפסות תלת מימד. קרדיט: © גרשון אלבר, מדעי המחשב, טכניון


