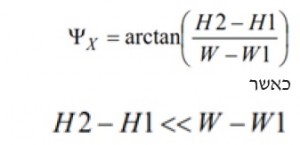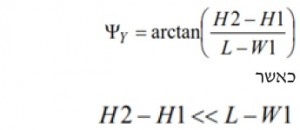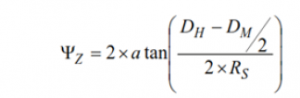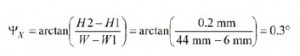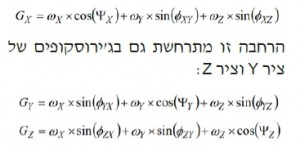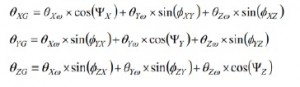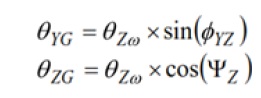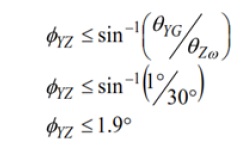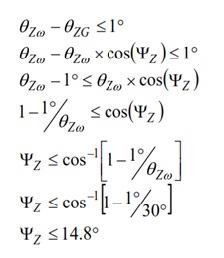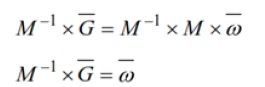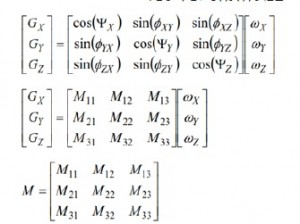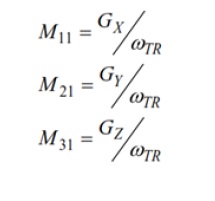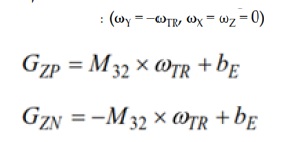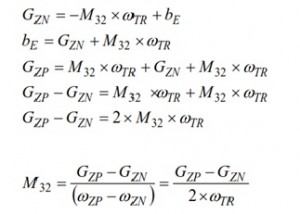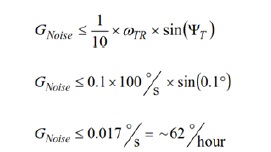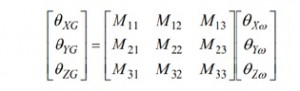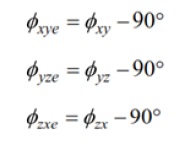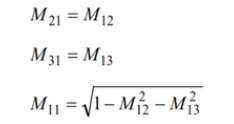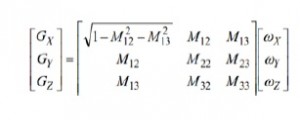יסודות כיוונון יחידות מדידה אינרטיות/ ג’ירוסקופ במערכת מיקרו אלקטרו מכנית

מכיוונון מוטעה של חיישן מהווה לעתים קרובות שיקול מפתח במערכות בקרת תנועה בעלות ביצועים גבוהים העושות שימוש ביחידות מדידה אינרטיות (Inertial Measurement Units -) במערכת מיקרו אלקטרו מכנית

( – Micro Electro Mechanical System) בלולאת המשוב שלהן. עבור הג’ירוסקופים ב-IMU כיוונון מוטעה של חיישן מתאר את ההפרש הזוויתי בין ציר הסיבוב של כל ג’ירוסקופ לבין המערכת, והוא מוגדר כמסגרת ייחוס אינרטית, הידועה גם כמסגרת גלובלית. ניהול ההשלכות של כיוונון מוטעה על דיוק החיישן, עשוי לדרוש אריזה ייחודית, תהליכי הרכבה מיוחדים, או אף בדיקות אינרטיות מורכבות בתצורה הסופית. לכל הדברים הללו עשויה להיות השפעה רבה על פרמטרים חשובים של ניהול פרויקט, כגון לוח זמנים, השקעות, והעלות הכוללת הקשורה ל-IMU בכל מערכת. אחרי הכל, אף אחד לא רוצה לשרוף 80% מלוח הזמנים והתקציב של הפרויקט ולגלות שהחיישנים הלא יקרים שלהם דורשים מאות, אולי אף אלפי דולרים בעלויות נוספות בלתי צפויות על מנת לעמוד במועדי מסירה בלתי ניתנים למשא ומתן ללקוחותיהם.

קיימות שלוש תפיסות כיוונונים בסיסיות להבנה ולהערכה של בניית הארכיטקטורה של פונקציית IMU עבור מערכת כלשהיא: הערכת שגיאה, הבנת השפעת כיוונון מוטעה על התנהגויות מפתח של מערכת, וכיוונון אלקטרוני (לאחר התקנה): הערכת שגיאה ראשונית צריכה לכלול תרומות לשגיאה מצד IMU ומצד המערכת המכנית המחזיקה אותה במקום בעת פעולה. הבנת ההשפעה של שגיאות אלו על פונקציות מפתח של מערכת, מסייעת בקביעת יעדי ביצוע רלבנטיים המונעים את הצורך בעבודת יתר על הבעיה, וגם מאפשרים לנהל באותה עת את הסיכון של החטאת התחייבויות מפתח של ביצוע ועלויות. ולבסוף, ייתכן כי נחוצה צורה כלשהיא של כיוונון אלקטרוני למיטוב (אופטימיזציה) של מרחב התחום של ביצועי מערכת/עלות מסחר.

ניבוי שגיאת כיוונון לאחר התקנה

דיוק הכיוונון ביישום כלשהוא, תלוי בשני גורמי מפתח: שגיאת הכיוונון של IMU ודיוק המערכת המכנית המחזיקה אותה במקום בעת פעולה. תרומת ה- (IMUΨ) וזו של המערכת (SYSΨ), אינן קשורות בדרך כלל האחת לשנייה, כך שהערכת שגיאת הכיוונון המוטעה הכוללת באה לעתים קרובות משילוב שני מקורות שגיאה אלו על ידי שימוש בחישוב השורש הריבועי של סכומם:

טבלאות מפרט IMU אחדות מכמתות שגיאות כיוונון מוטעה באמצעות פרמטרים כגון שגיאת כיוונון מוטעה של הציר לאריזה או שגיאת כיוונון מוטעה של הציר למסגרת. איור 1 מתאר מראה מוגזם של שגיאות כיוונון מוטעה אלו עבור כל ג’ירוסקופ ב-ADIS16485, ביחס לקצוות האריזה. באיור זה, הקווים הירוקים המקווקווים מייצגים את הצירים במסגרת הייחוס המוגדרת של האריזה. הקווים הרצופים מייצגים את ציר הסיבוב של הג’ירוסקופ שבתוך האריזה ו- IMUΨ מייצג את הערך המקסימלי של שלושת תנאי הכיוונון המוטעה (XΨ, YΨ, ZΨ).

ניבוי תרומת המערכת (SYSΨ במשוואה 1) לשגיאת הכיוונון המוטעה מצריכה ניתוח כל הזדמנות לחוסר שלמות מכנית העלולה להטות את מקום המנוחה של IMU במערכת ביחס למסגרת הגלובלית. כאשר משתמשים ב-IMU המולחם ללוח מעגל משולב, יהיה צורך בהתחשבות בדברים כגון דיוק מקום ההצבה המקורי, שינויים במקום הנחת הלַחַם, ציפה בעת זרימה מחודשת של הלַחַם, אפיצויות תכונות מפתח של המעגל המודפס (כגון חורי הרכבה), ואפיצויות מסגרת המערכת עצמה. כאשר משתמשים ב-IMU ברמת המודול, ייתכן צימוד יותר ישיר לקופסת המערכת, כמתואר באיור 2.

לממשק מסוג זה יש שתי תכונות מפתח מכניות המסייעות בניהול שגיאות הנובעות מסטייה בהרכבה: מדפי ההרכבה (4X), ובית ההרכבה בקופסה.

בסוג זה של תכנית הרכבה, שינוי בגובה ארבעת מדפי ההרכבה הנו דוגמה אחת לסטיית הרכבה בציר ה-X וציר ה-Y. איור 3 מביא תמונה מוגזמת על מנת לסייע בהסבר ההשלכה שיש לשינוי זה (H1 כנגד H2) על סטיית ההרכבה (XΨ), ביחס לציר ה-X.

איור 3. כיוונון מוטעה עקב שינוי במדף ההרכבה. משוואה 2 מספקת אפשרות לניבוי זווית הסטייה של ציר ה-X (XΨ) הקשורה להפרש בגובה (H1 כנגד H2) והרווח בין שתי נקודות המגע (W כנגד 1W):

השינוי בגובה מדפי ההרכבה ישפיע באופן דומה על סטיית ההרכבה סביב ציר ה-Y. במקרה זה, החלף את אורך האריזה (L) ברוחב (W) במשוואה 2 לפיתוח היחסים שלהלן בהערכת זווית הסטייה בציר ה-Y (YΨ).

איור 4 מספק דוגמה אחרת לאופן שבו תכונה מכנית עשויה להשפיע על סטיית ההרכבה סביב ציר ה-Z. במקרה זה, ברגי המכונה יחליקו דרך חורי ההרכבה בגוף ה-IMU (בכל ארבע הפינות), דרך חורים במדפי ההרכבה, ואז, לתוך אומי נעילה בצדם האחורי של מדפי ההרכבה. בתסריט זה, ההפרש בין קוטר ברגי המכונה (DM) וחורי המעבר הקשורים בהם (DH) בלוח הבסיס, מספקים הזדמנות לסטייה בציר ה-Z.

משוואה 4 מספקת אפשרות ניבוי ההזדמנות של סטיית הרכבה בציר ה-Z (ZΨ), על בסיס הפרש זה בין הקוטרים ורדיוס הסיבוב (Rs), אשר שווה לחצי המרחק בין שני ברגי ההרכבה בפינות הנגדיות.

 

דוגמה 1

הערך את הסטייה הכוללת הקשורה לשימוש בברגים בקוטר 2 מ”מ להרכבת ADIS16485 על מדפי ההרכבה במידות 6 מ”מ על 6 מ”מ, בעלי חורים במידות 2.85 מ”מ ואפיצות גובה של 0.2 מ”מ.

פתרון

באמצעות שימוש ברוחב (W) בעל גודל נקוב של 44 מ”מ, ניבוי זווית הסטייה של ציר ה-X (ראה איור 3), הנו 0 0.3.

הגודל הנקוב של המרחקים בין חורי ההרכבה בכל צד של אריזה זו הנם 39.6 מ”מ ו-42.6 מ”מ, בהתאם. ממדים אלו יוצרים את שני הצדדים של משולש ישר זווית, אשר ההיפוטנוזה שלו שווה למרחק בין שני החורים בפינות הנגדיות של האריזה. רדיוס הסיבוב (Rs, ראה איור 4) שווה לחצי מרחק זה (29.1 מ”מ), דבר המוביל לניבוי סטייה בציר ה-Z של 0 0.83.

עבור נוסחת הניבוי המרוכבת במשוואה 1, SYSΨ שווה ל-ZΨ (ערך המקסימום של ההערכות) ו-IMUΨ שווה ל-0 1, על פי ערך שגיאת הכיוונון המוטעה של הציר בדף הנתונים של IMU. הדבר מחולל כיוונון מוטעה כולל של 0 1.28.

השפעת כיוונון מוטעה על דיוק המערכת

הבנת היחסים הבסיסיים בין שגיאות כיוונון מוטעה וההשפעה שלהן על דיוק הג’ירוסקופ היא נקודה טובה להתחיל את תהליך פיתוח אמות מידה של דיוק עבור יישום. כדי להתחיל בתהליך זה, איור 5 מספק תמונה כללית של מערכת ג’ירוסקופ בעלת שלושה צירים. בתרשים זה, שלושת הקווים הרצופים הירוקים מייצגים את שלושת הצירים במסגרת הגלובלית, הקווים השחורים הרצופים מייצגים את צירי הסיבוב של כל שלושת הג’ירוסקופים, והתגים המבוססים על Ψ מייצגים את שגיאות הכיוונון המוטעה בין המסגרת הגלובלית וצירי הג’ירוסקופ. משוואות 5, 6 ו-7 מראות את ההשפעה של שגיאות הכיוונון המוטעה על התגובה של כל ג’ירוסקופ לסיבוב סביב הציר המיועד לו במסגרת הגלובלית. במשוואות אלו, הקוסינוס של זווית הכיוונון המוטעה מכניסה שגיאת סקאלה.

שגיאות כיוונון מוטעה מכניסות גם השפעות צולבות על גבי הצירים בכל ציר. כימות השפעות אלו מצריך פירוק זווית שגיאות הכיוונון המוטעה עבור כל ציר לשני רכיבים הקשורים לשני הצירים האחרים. לדוגמה, ל-XΨ יש רכיב בציר  (XYΦ) ורכיב בציר Z (), הגורמים להרחבה הבאה של תגובת הג’ירוסקופ של ציר X לסיבוב סביב כל שלושת הצירים במסגרת הגלובלית (ZωY, ω X,ω):

שילוב שני הצדדים של משוואות 8, 9 ו-10, יוצר יחסים דומים, המתבטאים במושגים של הסטת זווית. במשוואות 11, 12 ו-13 הנובעות מכך, הזוויות המעניינות אותנו הן זוויות הסטייה סביב המסגרת הגלובלית   והאינטגרציה של כל ג’ירוסקופ

דוגמה 2

כלי רכב בלתי מאויש (כרב”מ) משתמש ב-IMU של MEMS כחיישן משוב במערכת בקרת ייצוב פלטפורמה (platform stabilization control -) עבור האנטנה שלו. מערכת זו משתמשת בלולאת כַּוונַן (tuner) RSS אשר דורשת כי זוויות האזימות והגובה יישארו בתוך תחום של±1° על מנת לקיים תקשורת רצופה. בתנאים הדינמיים ביותר, מערכת PCS זו נשענת במידה רבה ביותר על מדידות הג’ירוסקופ בציר ה-Y למטרות בקרת זווית הגובה ועל מדידות הג’ירוסקופ בציר ה-Z למטרות בקרת זווית האזימות. השינוי המרבי בכיוון   בעת התנאים הדינמיים האלו הוא 0 30 ויש היעדר סיבוב סביב ציר ה-X או ציר ה-Y   בעת תמרון זה.

פתרון

היעדר סיבוב סביב ציר ה-X או ציר ה-Y מאפשר למשוואות 8 ו-9 להצטמצם למשוואות שלהלן:

החל מציר ה-Y, קבע תחום מרבי של 1° עבור  ופטור משוואה עבור ערך  של הכיוונון המוטעה. תהליך זה יוצר שגיאת כיוונון מוטעה מותרת מרבית של 1.9° עבור ג’ירוסקופ ציר Y.

עבור ציר ה-Z, קבע  שערכו שווה ל-0 30 וקבע  תחום מרבי של 1° עבור ההפרשים בין  ו-, ופטור עבור . תהליך זה קובע שגיאת כיוונון מוטעה מותרת מרבית של 14.8° עבור ג’ירוסקופ ציר Z.

חישובים אלו מגלים כי ההתנהגויות הצולבות בין ציר ה-X וציר ה-Y יניעו את דרישת דיוק הכיוונון של 1.9°~ עבור תסריט/תמרון ספציפי זה.

כיוונון אלקטרוני

במקרים בהם IMU והמערכת שלו לא יעמדו ביעדי מערכת קריטיים, כיוונון אלקטרוני מספק שיטה לצמצום שגיאות הכיוונון המוטעה. לתהליך זה שני שלבים: אפיין את תנאי הכיוונון המוטעה (לאחר התקנת ה-IMU) ופתח מטריצת כיוונון מתקנת המתקנת את הג’ירוסקופים על מנת להגיב כאילו הם היו מכווננים עם המסגרת הגלובלית כאשר זו מותקנת במערך הג’ירוסקופים. משוואה 14 מספקת דגם מערכת עבור תהליך זה, היכן שכניסות שלוש המערכות הנן הסיבוב סביב כל ציר במסגרת הגלובלית , יציאות המערכת הנן תגובות שלושת הג’ירוסקופים  , ומטריצה 3 X 3 () מייצגת את התנהגות המערכת (כולל כיוונון מוטעה) בין הכניסות והיציאות.

טיפול אלגבראי פשוט קובע כי התוצאה של מדידות הג’ירוסקופים  וההָפוך של  שווה למערך סיבוב המסגרת הגלובלית , לכן, מטריצת הכיוונון שווה ל-.

משוואות 8, 9 ו-10 מספקות את הבסיס להרחבת משוואה 14 להכללת תנאי הכיוונון המוטעה במשוואה 16, ובאופן יותר כללי, במשוואות 17 ו-18:

סיבוב המערכת כולה סביב ציר אחד בכל פעם, מפשט את דגם המערכת מספוק כדי לבודד כל רכיב במטריצה לאחת ממדידות הג’ירוסקופ. למשל, סיבוב המערכת סביב ציר X   תוך הענקת תשומת לב לכל שלושת הג’ירוסקופים, מסייע בפישוט היחסים עבור 11M, 21M ו-31M לאשר להלן:

ברור שלדיוק פרופיל התנועה  ומדידות הג’ירוסקופ  נודעת השפעה ישירה בתהליך זה. במיוחד התנועה מחוץ לציר עשויה להשפיע באופן משמעותי בתהליך זה כך שהיא צריכה להוות שיקול חשוב בעת הרכישה וההתקנה של ציוד בדיקה אינרטי אשר יעבוד על פי דרישות אלו. בנוגע לדיוק הג’ירוסקופ, ממתח ורעש מהווים שני איומים לדיוק, הדורשים בדרך כלל את לקיחתם בחשבון בעת תהליך זה. טכניקה אחת לניהול ההשפעה של שגיאת ממתח שיורית  במדידות הג’ירוסקופ, היא באמצעות שימוש בשני שיעורי סיבוב שונים אשר שווים ומנוגדים האחד לשני. למשל, כאשר מסובבים בכיוון החיובי סביב ציר Y , משוואה 28 מתארת את התגובה של הג’ירוסקופ בציר Z עם שגיאת ממתח. משוואה 29 מתארת את התגובה של הג’ירוסקופ בציר Z כאשר מסובבים סביב ציר Y בכיוון השלילי :

סדר משוואה 29 מחדש על מנת לייחס אותה לשגיאת הממתח , הכנס אותה במשוואה 28, ואז, פטור עבור 32M. שים לב כיצד שגיאת הממתח  יוצאת מהמשוואה.

נוסחה זו מניחה כי שגיאת הממתח קבועה בעת שתי המדידות, דבר אשר אינו ציפייה מציאותית, כך שיהיה נבון להבין את ההזדמנות לשינוי (טמפרטורה, זמן, ורעש) ממדידה למדידה. כאשר לוקחים את המדידות ברצף, בתנאי טמפרטורה יציבים, הרעש מהווה את שגיאת המפתח הדורשת ניהול בתהליך זה. רמת הרעש הקבילה במדידות הג’ירסקופ תהיה תלויה ביעד דיוק הכיוונון   ושיעור הסיבוב בכל ציר בעת האיפיון . טכניקה נפוצה לצמצום רעש היא באמצעות מיצוע רשומות הזמן של נתוני הג’ירוסקופ תוך שמירת התנאים האינרטיים קבועים. עקומות שינויי Allan מספקות כלי להבנת התהליך של תן וקח בין חזרתיות (רעש) והזמן הממוצע.

דוגמה 3

אם שיעור הסיבוב בעת האיפיון הנו 1000/s, יעד דיוק הכיוונון הוא 0 10, והרעש (rms) צריך להיות 10X פחות מיעד הכיוונון המוטעה, לכמה זמן אנו זקוקים כדי לבצע ממוצע של יציאות ה-ADIS16485 על מנת להשיג יעדים אלו?

פתרון

בשימוש בתגובה כללית בין הג’ירוסקופ והכניסה (סיבוב על פלטפורמת הבדיקה), החישובים הבאים מראים כי הרעש הכולל (rms) בכל ג’ירוסקופ צריך להיות פחות

מ-0  62 לשעה.

באיור 6 מובאת דוגמה לאופן בו יש להשתמש בעקומת שינוי Allan עבור IMU זה כדי לבחור זמן ממוצע לעמידה בדרישה זו. במקרה זה, זמן ממוצע של 0.1 שניות עומד ביעד ה-0  62 לשעה עבור החזרתיות, עם שוליים מסוימים. שים לב כי גישה זו מתייחסת רק לרעש בחיישן עצמו. אם קיימות רעידות בפלטפורמה אשר מוסיפות רעש למדידות הג’ירוסקופ, יש צורך בשיקולים וסינון נוספים.

טיפים וטריקים לפישוט התהליך

פיתוח מערכת תלת-צירית אינרטית בעלת הדיוק ובקרת טמפרטורת הסביבה הנחוצים, דורש בדרך כלל השקעה משמעותית בהון, בציוד, ובמשאבי פיתוח הנדסיים. לאלה המפתחים מערכות דור ראשון או שני המציבות שאלות רבות בעת הפיתוח, ייתכן כי סוגים אלו של משאבים וזמן לא יהיו בהישג יד. מצב זה יוצר צורך בפתרון פשוט יותר, העשוי לבוא דרך בחירה זהירה של IMU ומינוף תנועה טבעית הקיימת במכשיר או ביישום.

לדוגמה, לפעמים, עבודה עם זוויות עשויה להיות יותר נוחה מעבודה עם מדידות שיעור זוויתי. משוואה 31 משלבת משוואות 11, 12 ו-13 בייצוג התנהגויות מערכת (M) במושגים של זוויות סביב המסגרת הגלובלית  ומתוך הכללת יציאות הג’ירוסקופים  :

בנוגע לבחירת ההתקן, שגיאת כיוונון מוטעה מציר לציר מהווה פרמטר מפתח לשיקול, כיוון שכאשר היא נמוכה מפרמטר הכיוונון המוטעה של הציר לאריזה, הוא עשוי לסייע בהורדת מורכבות פרופיל הבדיקה האינרטית (במשוואה 16) הקשורה לכיוונון האלקטרוני. בעוד פרמטר הכיוונון המוטעה של הציר לאריזה מתאר את כיוון הג’ירוסקופ ביחס לנקודת ייחוס מכנית חיצונית, פרמטר הכיוונון המוטעה של הציר לאריזה מקשר את הכיוון של כל ג’ירוסקופ ביחס לשני הג’ירוסקופים האחרים. לעתים קרובות ביותר, הכיוון האידיאלי עבור שלושת הג’ירוסקופים בתוך IMU של MEMS הוא ˚90 אחד מהשני, כך שפרמטר הכיוונון המוטעה של ציר לציר קשור לפרמטר נפוץ אחר עבור התנהגות צולבת צירים זו. שימוש באיור 7 כנקודת ייחוס, ייצג את המקסימום של שלושת היחסים שלהלן:

פרמטר כיוונון מוטעה ציר לציר קובע את השגיאה הקשורה להנחה כי לחיישנים יש כיוונון אורתוגונלי מושלם בעת פיתוח תהליך כיוונון אלקטרוני. באמצעות שימוש בהנחת כיוונון אורתוגונלי מושלם, ניתן לכוונן את כל שלושת הצירים דרך שני צירי סיבוב בלבד. למשל, סיבוב סביב ציר Y ו-Z, מאפשר צפייה ישירה ב-12M, 13M, 22M, 23M, 32M ו-33M. הנחת כיוונון אורתוגונלי מושלם ויישום תכונות טריגונומטריות מסוימות, מאפשרים חישוב של שלושת האלמנטים האחרים באמצעות שימוש בששה אלמנטים וביחסים הבאים:

זהויות אלו מביאות לעדכון הבא בדגם המערכת, היכן שכל תשעת האלמנטים במטריצת M מבוטאים במושגים של ששת האלמנטים הנובעים מסיבוב ציר Y וציר Z.

מסקנה

טכנולוגיה MEMS אינרטית השיגה התקדמות מדהימה בשנים האחרונות, העניקה למפתחי מערכות קשת רחבה של אופציות בתוך מרחב מסחרי מורכב הכולל גודל, משקל, הספק, עלות יחידה, עלות אינטגרציה וביצועים. עבור אלו הבונים ארכיטקטורה של מערכות בקרת תנועה עם IMU של MEMS בפעם הראשונה, יש דברים רבים ללמוד בנוגע לבחירה נכונה של IMU ולהכנת תמיכה בדרישות מערכת קריטיות עם IMU זה. מאחר שלדיוק הכיוונון עשויה להיות השפעה משמעותית בביצועים קריטיים, עלות ויעדי לוחות זמנים, זהו שיקול חשוב. אפילו כלי ניתוח פשוטים יכולים לסייע בזיהוי פריטים בלעי סיכון פוטנציאלי בשלבי התכנון הקונספטואלי והארכיטקטוני, כאשר יש עוד זמן להשפיע על בחירת ההתקנים, התכנון המכני, הכיול שלאחר ההרכבה (כינון אלקטרוני), על צפי עלות ראשוני, ואבני דרך מפתח בלוחות הזמנים. אם לוקחים זאת אף רחוק יותר, אחרים ימצאו חשיבות בהכרת ערכי מפתח של מדידות IMU ובהזדמנות להחליף ציוד בדיקה אינרטית תלת-צירית עם תנועה טבעית הזמינה במערכת שלהם להשגת התמורה הטובה ביותר (ביצוע, עלות כוללת של התקנה) מהמערכת שלהם.